
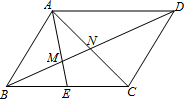
 如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )
如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 以上都不正确 |
分析 由?ABCD,推出AD∥BE,BN=ND,进而推得△ADM∽△EBM,根据相似三角形的性质和E为BC的中点可证得$\frac{BM}{MD}$=$\frac{1}{2}$,即可证得结论.
解答 解:∵?ABCD,
∴AD∥BE,AD=BC,BN=ND,
∴△ADM∽△EBM,
∴$\frac{BM}{MD}=\frac{BE}{AD}$,
∵E为BC的中点,
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
∴$\frac{BM}{MD}$=$\frac{1}{2}$,
设BM=1,则MD=2,BD=3,
∴DN=$\frac{3}{2}$,
∴$\frac{BM}{DN}$=$\frac{1}{\frac{3}{2}}$=$\frac{2}{3}$,
故选C.
点评 本题主要考查了平行四边形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图是汽车加油站在加油过程中,加油器仪表某一瞬间的显示,请你结合图片信息,解答下列问题:
如图是汽车加油站在加油过程中,加油器仪表某一瞬间的显示,请你结合图片信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
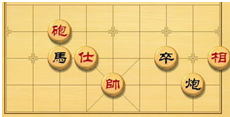 象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种.由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.如图是一方的棋盘,如果“帅”的坐标是(0,1),“卒”的坐标是(2,2),那么“马”的坐标是( )
象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种.由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.如图是一方的棋盘,如果“帅”的坐标是(0,1),“卒”的坐标是(2,2),那么“马”的坐标是( )| A. | (-2,1) | B. | (2,-2) | C. | (-2,2) | D. | (2,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com