
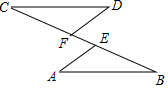
 如图,点C、F、E、B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
如图,点C、F、E、B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论. 分析 求出CF=BE,根据SAS证△AEB≌△CFD,推出CD=AB,∠C=∠B,根据平行线的判定推出CD∥AB.
解答 解:CD∥AB,CD=AB,
理由是:∵CE=BF,
∴CE-EF=BF-EF,
∴CF=BE,
在△AEB和△CFD中,
$\left\{\begin{array}{l}{CF=BE}\\{∠CFD=∠BEA}\\{DF=AE}\end{array}\right.$,
∴△AEB≌△CFD(SAS),
∴CD=AB,∠C=∠B,
∴CD∥AB.
点评 本题考查了平行线的判定和全等三角形的性质和判定的应用.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.


科目:初中数学 来源: 题型:选择题
| A. | x≥-2 | B. | x≤-2 | C. | x≥1 | D. | x≥-2 且x≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
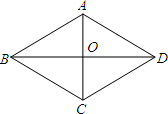 求证:对角线互相垂直的平行四边形是菱形.
求证:对角线互相垂直的平行四边形是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 城市 | 悉尼 | 纽约 |
| 时差/时 | +2 | -13 |
| A. | 6月16日1时;6月15日10时 | B. | 6月16日1时;6月14日10时 | ||
| C. | 6月15日21时;6月15日10时 | D. | 6月15日21时;6月16日12时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知矩形ABCD(AB<AD).
如图,已知矩形ABCD(AB<AD).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com