
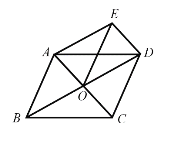
【题目】如图,点P在⊙O的直径BA延长线上,PC与⊙O相切,切点为C,点D在⊙O上,连接PD、BD,已知PC=PD=BC.下列结论:
①PD与⊙O相切;
②四边形PCBD是菱形;
③PO=AB;
④∠PDB=120°.
其中,正确的个数是( )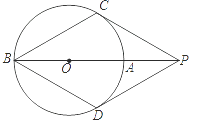
A.4个
B.3个
C.2个
D.1个
【答案】A
【解析】解:①连接CO,DO,
∵PC与⊙O相切,切点为C,
∴∠PCO=90°,
在△PCO和△PDO中,
∵ 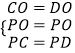 ,
,
∴△PCO≌△PDO(SSS),
∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,
故①正确;
②由①得:∠CPB=∠BPD,
在△CPB和△DPB中,
∵ 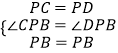 ,
,
∴△CPB≌△DPB(SAS),
∴BC=BD,
∴PC=PD=BC=BD,
∴四边形PCBD是菱形,
故②正确;
③连接AC,
∵PC=CB,
∴∠CPB=∠CBP,
∵AB是⊙O直径,
∴∠ACB=90°,
在△PCO和△BCA中,
∵ 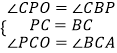 ,
,
∴△PCO≌△BCA(ASA),
∴AC=CO,
∴AC=CO=AO,
∴∠COA=60°,
∴∠CPO=30°,
∴CO= ![]() PO=
PO= ![]() AB,
AB,
∴PO=AB,
故③正确;
④∵四边形PCBD是菱形,∠CPO=30°,
∴DP=DB,则∠DPB=∠DBP=30°,
∴∠PDB=120°,
故④正确;
正确个数有4个,
故答案为:A.
①连接CO,DO,在△PCO和△PDO中,根据边边边可得△PCO≌△PDO,由全等三角形的性质可得∠PCO=∠PDO=90°,根据切线的判断可得PD与⊙O相切,则①符合题意;在△CPB和△DPB中,根据边角边可证△CPB≌△DPB,则BC=BD,结合已知条件可得PC=PD=BC=BD,由菱形的判定可得四边形PCBD是菱形,所以②符合题意;在△PCO和△BCA中,用角边角可证△PCO≌△BCA,由全等三角形的性质可得AC=CO,那么有AC=CO=AO,所以∠COA=60°,∠CPO=30°,根据直角三角形中,30度角所对的直角边等于斜边的一半可得CO= ![]() PO=
PO= ![]() AB,所以PO=AB,故③符合题意;根据四边形PCBD是菱形可得DP=DB,结合∠CPO=30°可得∠DPB=∠DBP=30°,则∠PDB=120°,所以④符合题意。所以符合题意的选项是A。
AB,所以PO=AB,故③符合题意;根据四边形PCBD是菱形可得DP=DB,结合∠CPO=30°可得∠DPB=∠DBP=30°,则∠PDB=120°,所以④符合题意。所以符合题意的选项是A。


科目:初中数学 来源: 题型:
【题目】某校为了增强学生对中华优秀传统文化的理解,决定购买一批相关的书籍.据了解,经典著作的单价比传说故事的单价多6元,用10000元购买经典著作与用7000元购买传说故事的本数相同,这两类书籍的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
, ![]() ,
,![]() ,
,![]() , 垂足为
, 垂足为![]() ,在平行四边形的边上有一点
,在平行四边形的边上有一点![]() ,且
,且![]() .将平行四边形折叠,使点
.将平行四边形折叠,使点![]() 与点
与点![]() 合,折痕所在直线与平行四边形交于点
合,折痕所在直线与平行四边形交于点![]() 、
、![]() .
.
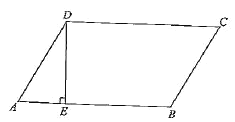
(1)求![]() 的长;
的长;
(2)请补全图形并求折痕![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太仓港区道路绿化工程工地有大量货物需要运输,某车队有载重量为8吨和10吨的卡车共15辆,所有车辆运输一次能运输128吨货物.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的扩大,车队需要一次运输货物170吨以上,为了完成任务,车队准备增购这两种卡车共5辆(两种车都购买),请写出所有可能的购车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC;②∠EDA=∠B;③OA= ![]() AC;④DE是⊙O的切线,正确的个数是( )
AC;④DE是⊙O的切线,正确的个数是( )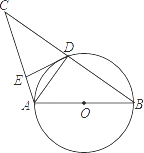
A.1 个
B.2个
C.3 个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在行驶完某段全程600千米的高速公路时,李师傅对张师傅说:“你的车速太快了,平均每小时比我多跑20千米,比我少用1.5小时就跑完了全程.”
(1)若这段高速公路全程限速120千米/小时,两人全程均匀速行驶.那么张师傅超速了吗?请说明理由;
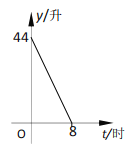
(2)张师傅所行驶的车内油箱余油量![]() (升)与行驶时间
(升)与行驶时间![]() (时)的函数关系如图所示,则行驶完这段高速公路,他至少需要多少升油?
(时)的函数关系如图所示,则行驶完这段高速公路,他至少需要多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。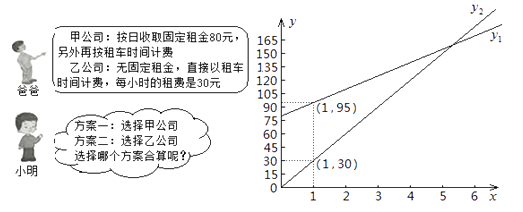
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形 ABCD 的对角线 AC、BD 交于 O 点,AE∥BD,∠AED=∠AOD,连接 OE.
(1)求证:AE=OB;
(2)求证:四边形 CDEO 是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com