
【题目】已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?(![]() ,
,![]() ,
,![]() )
)
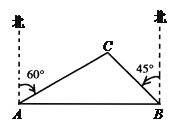
【答案】3小时.
【解析】
作CD⊥AB于D点.设CD=x海里,在直角△ACD中,利用x表示出AC,AD,同理表示出BD,BC,根据AB=40即可列出方程求得CD的长,则AC+CB即可求得,然后除以速度即可得到时间.
作CD⊥AB于D点.设CD=x海里,
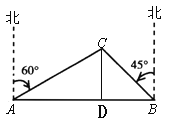
在直角△ACD中,∠CAD=90°-60°=30°,
则AC=2x,AD=![]() x,
x,
在直角△BCD中,∠CBD=45°,
则BD=CD=x,BC=![]() CD=
CD=![]() x,
x,
∵AB=40,即AD+BD=40,
∴![]() x+x=40,
x+x=40,
解得:x=20(![]() -1),
-1),
∴BC=20![]() (
(![]() -1)=20
-1)=20![]() -20
-20![]() ,AC=2x=40(
,AC=2x=40(![]() -1),
-1),
则总路程是:20![]() -20
-20![]() +40(
+40(![]() -1)海里,
-1)海里,
则时间是:![]() (小时).
(小时).
∵该船在C岛停留半个小时,
∴需要3小时能把这批物资送到A港.
考点: 解直角三角形的应用-方向角问题.


科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是
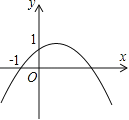
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果三角形的两个内角![]() 与
与![]() 满足
满足![]() ,那么称这样的三角形为“类直角三角形”.
,那么称这样的三角形为“类直角三角形”.
尝试运用
(1)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线.
的平分线.
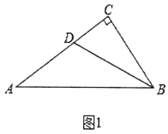
①证明![]() 是“类直角三角形”;
是“类直角三角形”;
②试问在边![]() 上是否存在点
上是否存在点![]() (异于点
(异于点![]() ),使得
),使得![]() 也是“类直角三角形”?若存在,请求出
也是“类直角三角形”?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
类比拓展
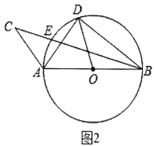
(2)如图2,![]() 内接于
内接于![]() ,直径
,直径![]() ,弦
,弦![]() ,点
,点![]() 是弧
是弧![]() 上一动点(包括端点
上一动点(包括端点![]() ,
,![]() ),延长
),延长![]() 至点
至点![]() ,连结
,连结![]() ,且
,且![]() ,当
,当![]() 是“类直角三角形”时,求
是“类直角三角形”时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,□ABCD的对角线AC,BD相交于点O,E、F、G、H分别是OA、OB、OC、OD的中点,那么□ABCD与四边形EFGH是否是位似图形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
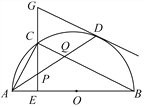
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度![]() 时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到
时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到![]() 时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至
时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至![]() 时,制冷再次停止,……,按照以上方式循环进行.
时,制冷再次停止,……,按照以上方式循环进行.
同学们记录了44![]() 内15个时间点冷柜中的温度
内15个时间点冷柜中的温度![]() 随时间
随时间![]() 的变化情况,制成下表:
的变化情况,制成下表:

(1)通过分析发现,冷柜中的温度![]() 是时间
是时间![]() 的函数.
的函数.
①当![]() 时,写出一个符合表中数据的函数解析式 ;
时,写出一个符合表中数据的函数解析式 ;
②当![]() 时,写出一个符合表中数据的函数解析式 ;
时,写出一个符合表中数据的函数解析式 ;
(2)![]() 的值为 ;
的值为 ;
(3)如图,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余对应的点,并画出![]() 时温度
时温度![]() 随时间
随时间![]() 变化的函数图象.
变化的函数图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,已知点
放置在平面直角坐标系中,已知点![]() ,点
,点![]() ,点
,点![]() .
.![]() 是边
是边![]() 上的一动点(点
上的一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),沿着
重合),沿着![]() 折叠该纸片,得点
折叠该纸片,得点![]() 的对应点
的对应点![]() .
.
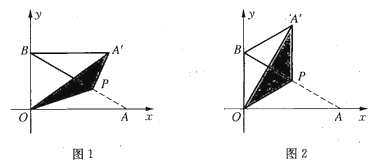
(1)如图1,当点![]() 在第一象限,且满足
在第一象限,且满足![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,当![]() 为
为![]() 中点时,求
中点时,求![]() 的长;
的长;
(3)当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com