
【题目】如图,一次函数y=ax+b与反比例函数y=![]() (x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(1)求反比例函数和一次函数的表达式;
(2)根据图像直接说出不等式ax+b-![]() <0的解集为______;
<0的解集为______;
(3)求△ABC的面积.
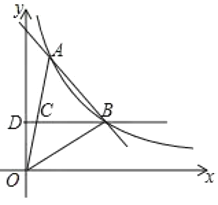
【答案】(1)y=-x+6;y=![]() ;(2)0<x<2或x>4;(3)S△ABC=3.
;(2)0<x<2或x>4;(3)S△ABC=3.
【解析】
(1)此处由题意可先求出反比例函数表达式,再根据CO=CA设出A点坐标求出A点坐标,代入即可求出一次函数表达式.
(2)此处根据数形结合找出一次函数与反比例函数关系即可.
(3)此题可先求出C点坐标,根据A,B,C三点坐标求面积即可.
(1)如图,过点A作AF⊥x轴交BD于E,
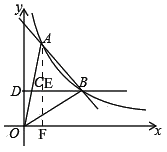
∵点B(4,2)在反比例函数y=![]() 的图象上,
的图象上,
∴k=4×2=8,
∴反比例函数的表达式为y=![]() ,
,
∵B(4,2),
∴EF=2,
∵BD⊥y轴,OC=CA,
∴AE=EF=![]() AF,
AF,
∴AF=4,
∴点A的纵坐标为4,
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴A(2,4),
∴4a+b=2;2a+b=4,
∴a=-1 b=6,
∴一次函数的表达式为y=-x+6;
(2)0<x<2或x>4.
(3)如图1,过点A作AF⊥x轴于F交OB于G,
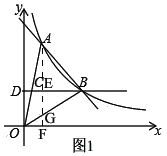
∵A(2,4),
∴直线OA的解析式为y=2x,
∴C(1,2),
∵A(2,4),
∴AE=4-2=2,BC=4-1=3,
∴S△ABC=![]() ×2×3=3.
×2×3=3.


科目:初中数学 来源: 题型:
【题目】在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E、F分别在边
,点E、F分别在边![]() 、
、![]() 上,
上,![]() ,点P与
,点P与![]() 在直线
在直线![]() 的两侧,
的两侧,![]() ,
,![]() ,射线
,射线![]() 、
、![]() 与边
与边![]() 分别相交于点M、N,设
分别相交于点M、N,设![]() ,
,![]() .
.
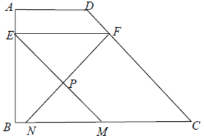
(1)求边![]() 的长;
的长;
(2)如图,当点P在梯形![]() 内部时,求关于x的函数解析式,并写出定义域;
内部时,求关于x的函数解析式,并写出定义域;
(3)如果![]() 的长为2,求梯形
的长为2,求梯形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
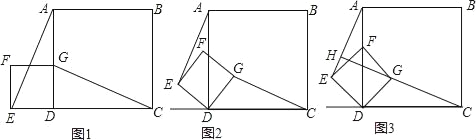
【题目】(1)如图1,正方形ABCD和正方形DEFG,G在AD边上,E在CD的延长线上.求证:AE=CG,AE⊥CG;
(2)如图2,若将图1中的正方形DEFG绕点D顺时针旋转角度θ(0°<θ<90°),此时AE=CG还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,当正方形DEFG绕点D顺时针旋转45°时,延长CG交AE于点H,当AD=4,DG=![]() 时,求线段CH的长.
时,求线段CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
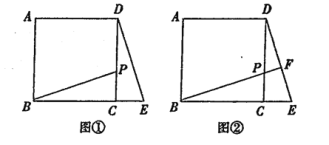
【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连结BP.将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D,旋转的角度是 度.
应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②.求∠BFE的度数.
拓展:如图②,若DP=2CP,BC=3,则四边形ABED的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
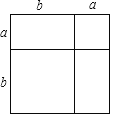
【题目】如图所示的大正方形是由两个小正方形和两个长方形组成.
(1)通过两种不同的方法计算大正方形的面积,可以得到一个数学等式;
(2)利用(1)中得到的结论,解决下面的问题:若a+b=2,ab=﹣3,
求:①a2+b2;
②a4+b4.
查看答案和解析>>
科目:初中数学 来源: 题型:
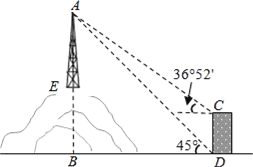
【题目】如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.若小山高BE=62m,楼的底部D与山脚在同一水平面上,求铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干块如左图所示的正方形或长方形纸片拼成图(1)和图(2)
(1)如图(1),若AD=7,AB=8,求![]() 与
与![]() 的值;
的值;
(2)如图(1),若长方形ABCD的面积为35,其中阴影部分的面积为20,求长方形ABCD的周长;
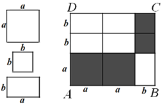
图(1)
(3)如图(2),若AD的长度为5,AB的长度为![]() .
.
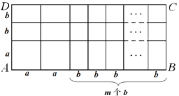
图(2)
①当![]() =________,
=________,![]() =_________时,
=_________时,![]() ,
,![]() 的值有无数组;
的值有无数组;
②当![]() ________,
________,![]() _________时,
_________时,![]() ,
,![]() 的值不存在.
的值不存在.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com