
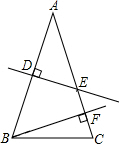
 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )| A. | 30° | B. | 35° | C. | 45° | D. | 36° |
分析 先根据等腰三角形的性质得出∠ABC=∠C,再由垂直平分线的性质得出∠A=∠ABE,根据CE的垂直平分线正好经过点B,与AC相交于点可知△BCE是等腰三角形,故BF是∠EBC的平分线,故$\frac{1}{2}$(∠ABC-∠A)+∠C=90°,把所得等式联立即可求出∠A的度数.
解答 解:∵△ABC是等腰三角形,
∴∠ABC=∠C=$\frac{180°-∠A}{2}$①,
∵DE是线段AB的垂直平分线,
∴∠A=∠ABE,
∵CE的垂直平分线正好经过点B,与AC相交于点可知△BCE是等腰三角形,
∴BF是∠EBC的平分线,
∴$\frac{1}{2}$(∠ABC-∠A)+∠C=90°,即$\frac{1}{2}$(∠C-∠A)+∠C=90°②,
①②联立得,∠A=36°.
故∠A=36°,
故选D.
点评 本题考查的是线段垂直平分线的性质及等腰三角形的性质,解答此类问题时往往用到三角形的内角和为180°这一隐含条件.


科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大3倍 | C. | 扩大6倍 | D. | 缩小到原来的$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
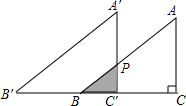 如图所示,BC=$\sqrt{2}$,先将△ABC与△A′B′C′,完全重合,再将△ABC固定,△A′B′C′沿CB所在的直线向左移动,当△ABC与△A′B′C′的重叠部分的面积是△ABC一半时,则△A′B′C′平移的距离是$\sqrt{2}-$1.
如图所示,BC=$\sqrt{2}$,先将△ABC与△A′B′C′,完全重合,再将△ABC固定,△A′B′C′沿CB所在的直线向左移动,当△ABC与△A′B′C′的重叠部分的面积是△ABC一半时,则△A′B′C′平移的距离是$\sqrt{2}-$1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-2)2=2 | B. | (x-2)2=4 | C. | (x-2)2=1 | D. | (x-2)2=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com