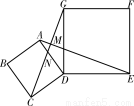
如图，四边形ABCD、DEFG都是正方形，连接AE、CG,AE与CG相交于点M，CG与AD相交于点N。求证: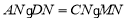
见解析
【解析】
试题分析：首先根据正方形的性质得到AD=CD，DE=DG，∠ADC=∠EDG，从而可以得到∠ADE=∠CDG，可以得到△ADE≌△CDG，根据全等得到∠DAE=∠DCG，再加上对顶角∠ANM=∠CND得到△AMN∽△CDN，从而说明所要证明的结论.
试题解析：∵四边形ABCD和四边形DEFG都是正方形，∴AD=CD，DE=DG，∠ADC=∠EDG=90°，
∵∠ADE=90°+∠ADG，∠CDG=90°+∠ADG，∴∠ADE=∠CDG， ∴△ADE≌△CDG（SAS），
∴∠DAE=∠DCG， 又∵∠ANM=∠CND， ∴△AMN∽△CDN， ∴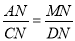
，
即AN•DN = CN•MN．
考点：
科目：初中数学 来源：2014-2015学年湖北省容城镇三闾学校九年级上学期期中考试数学试卷（解析版） 题型：填空题
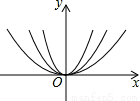
如图所示,在同一坐标系中,作出①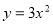
②
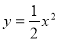③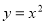
的图象,则图象从里到外的三条抛物线对应的函数依次是（填序号） 。
查看答案和解析>>
科目：初中数学 来源：2014-2015学年北京市燕山区九年级上学期期末考试数学试卷（解析版） 题型：填空题
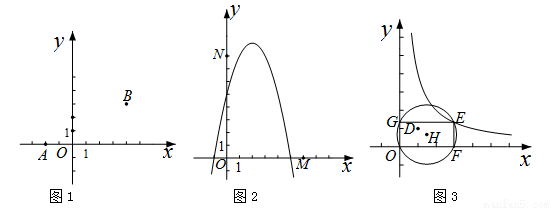
在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：
若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的外延矩形．点A，B，C的所有外延矩形中，面积最小的矩形称为点A，B，C的最佳外延矩形．例如，图中的矩形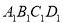
，
，
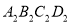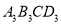都是点A，B，C的外延矩形，矩形
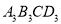是点A，B，C的最佳外延矩形．
（1）如图1，已知A（－2，0），B（4，3），C（0，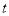
）．
①若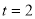
，则点A，B，C的最佳外延矩形的面积为 ；
②若点A，B，C的最佳外延矩形的面积为24，则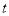的值为 ；
（2）如图2，已知点M（6，0），N（0，8）．P（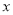
，
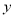）是抛物线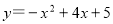
上一点，求点M，N，P的最佳外延矩形面积的最小值，以及此时点P的横坐标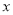的取值范围；
（3）如图3，已知点D（1，1）．E（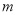
，
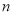）是函数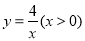
的图象上一点，矩形OFEG是点O，D，E的一个面积最小的最佳外延矩形，⊙H是矩形OFEG的外接圆，请直接写出⊙H的半径r的取值范围．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年北京市燕山区九年级上学期期末考试数学试卷（解析版） 题型：选择题
如图，在Rt△OAB中，∠AOB＝90°，OA＝4，OB＝3．⊙O的半径为2，点P是线段AB上的一动点，过点P作⊙O的一条切线PQ，Q为切点．设AP＝
，PQ2＝
，则与的函数图象大致是
查看答案和解析>>
科目：初中数学 来源：2014-2015学年北京市通州区九年级上学期期末考试数学试卷（解析版） 题型：填空题
已知反比例函数图象经过点（－1，3），那么这个反比例函数的表达式为_______________.
查看答案和解析>>
科目：初中数学 来源：2014-2015学年北京市通州区九年级上学期期末考试数学试卷（解析版） 题型：选择题
如图，为了测楼房BC的高，在距离楼房10米的A处，测得楼顶B的仰角为α，那么楼房BC的高为（ ）
A．10tanα（米） B．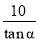
（米） C．10sinα（米） D．
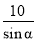（米）
查看答案和解析>>
科目：初中数学 来源：2014-2015学年北京市海淀区九年级上学期期末考试数学试卷（解析版） 题型：解答题
在平面直角坐标系
中，反比例函数
的图象经过点
，
．
（1）求代数式mn的值；
（2）若二次函数
的图象经过点B，求代数式
的值；
（3）若反比例函数
的图象与二次函数
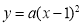的图象只有一个交点，且该交点在直线
的下方，结合函数图象，求
的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，求代数式
的值．