
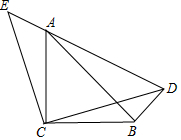
 如图,等腰直角△ECD的斜边为6,点A从点E出发,沿射线ED以每秒一个单位的速度运动,连接AC过点C作BC⊥AC,且AC=BC,连接AB,BD,运动1秒钟.
如图,等腰直角△ECD的斜边为6,点A从点E出发,沿射线ED以每秒一个单位的速度运动,连接AC过点C作BC⊥AC,且AC=BC,连接AB,BD,运动1秒钟.分析 (1)如图1中,当EA=AD时,即t=3s时,四边形ACBD是正方形;
(2)分两种情形分别讨论即可:①如图2中,当0<t<6时,②如图3中,当t>6时,分别求解即可;
解答 解:(1)如图1中,当EA=AD时,即t=3s时,四边形ACBD是正方形.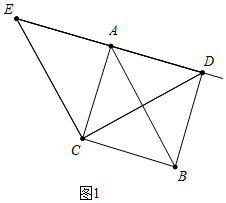
理由:∵CE=CD,AE=AD,∠ECD=45°,
∴CA⊥DE,CA=AD=BC,
∵∠ACB=∠CAD=90°,
∴∠ACB+∠CAD=180°,
∴AD∥BC,
∴四边形ACBD 是平行四边形,
∵AC=BC,∠ACB=90°,
∴四边形ACBD是正方形.
即t=3s时,四边形ACBD是正方形.
(2)①如图2中,当0<t<6时,
∵∠ECD=∠ACB=90°,
∴∠ECA=∠DCB,
∵CE=CD,CA=CB,
∴△ECA≌△DCB,
∴S△ECA=S△DCB,
∴S四边形ACBD=S△ECD=9,
②如图3中,当t>6时,作CH⊥DE于H.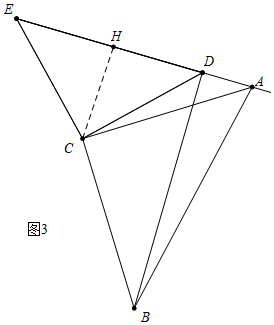
易知CH=EH=DH=3,
S四边形ADBC=S△ADC+S△ACB=$\frac{1}{2}$•(t-6)•3+$\frac{1}{2}$•[32+(t-3)2]=$\frac{1}{2}$t2-$\frac{3}{2}$t.
综上所述,S=$\left\{\begin{array}{l}{9}&{(0<t<6)}\\{\frac{1}{2}{t}^{2}-\frac{3}{2}t}&{(t>6)}\end{array}\right.$.
点评 本题考查等腰直角三角形的性质.正方形的判定和性质、四边形的面积等知识,解题的关键是正确寻找全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
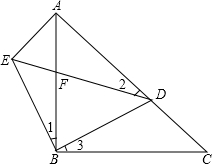 如图,三角形ABC,AB=BC,∠ABC=90°,∠1=∠2=∠3,
如图,三角形ABC,AB=BC,∠ABC=90°,∠1=∠2=∠3,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
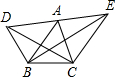 如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )
如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )| A. | ${S_2}=\frac{3}{2}({S_1}+{S_3})$ | B. | ${S_2}=\frac{1}{2}({S_3}-{S_1})$ | C. | ${S_2}=\frac{1}{2}({S_1}+{S_3})$ | D. | ${S_2}=\frac{3}{2}({S_3}-{S_1})$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它是数轴上离原点$\sqrt{10}$个单位长度的点表示的数 | |
| B. | 它是一个无理数 | |
| C. | 若a<$\sqrt{10}$<a+1,则整数a为3 | |
| D. | 它表示面积为10的正方形的边长 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 200元,240元 | B. | 240元,200元 | C. | 280元,160元 | D. | 160元,280元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com