
【题目】随着“中国诗词大会”节目的热播,《唐诗宋词精选》一书也随之热销.如果一次性购买10本以上,超过10本的那部分书的价格将打折,并依此得到付款金额y(单位:元)与一次性购买该书的数量x(单位:本)之间的函数关系如图所示,则下列结论错误的是( )
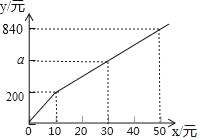
A. 一次性购买数量不超过10本时,销售价格为20元/本
B. a=520
C. 一次性购买10本以上时,超过10本的那部分书的价格打八折
D. 一次性购买20本比分两次购买且每次购买10本少花80元
【答案】D
【解析】
A、根据单价=总价÷数量,即可求出一次性购买数量不超过10本时,销售单价,A选项正确;C、根据单价=总价÷数量结合前10本花费200元即可求出超过10本的那部分书的单价,用其÷前十本的单价即可得出C正确;B、根据总价=200+超过10本的那部分书的数量×16即可求出a值,B正确;D,求出一次性购买20本书的总价,将其与400相减即可得出D错误.此题得解.
解:A、∵200÷10=20(元/本),
∴一次性购买数量不超过10本时,销售价格为20元/本,A选项正确;
C、∵(840﹣200)÷(50﹣10)=16(元/本),16÷20=0.8,
∴一次性购买10本以上时,超过10本的那部分书的价格打八折,C选项正确;
B、∵200+16×(30﹣10)=520(元),
∴a=520,B选项正确;
D、∵200×2﹣200﹣16×(20﹣10)=40(元),
∴一次性购买20本比分两次购买且每次购买10本少花40元,D选项错误.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
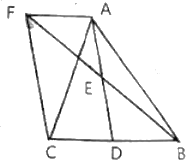
(1)四边形AFCD是什么特殊的四边形?请说明理由.
(2)填空:
①若AB=AC,则四边形AFCD是_______形.
②当△ABC满足条件______时,四边形AFCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
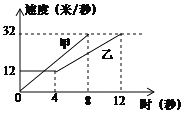
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A,点B,点C表示的数分别为-2,1,6.![]()
(1)线段AB的长度为___个单位长度,线段AC的长度为____个单位长度.
(2)点P是数轴上的一个动点,从A点出发,以每秒1个单位长度的速度,沿数轴的正方向运动,运动时间为t秒(0≤t≤8).用含t的代数式表示:线段BP的长为—个单位长度,点P在数轴上表示的数为___;
(3)点M,点N都是数轴上的动点,点M从点A出发以每秒4个单位长度的速度运动,点N从点C出发以每秒3个单位长度的速度运动.设点M,N同时出发,运动时间为x秒.点M,N相向运动,当点M,N两点间的距离为13个单位长度时,求x的值,并直接写出此时点M在数轴上表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=8cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当一个点到达终点时,另一个点随之停止.设运动时间为x秒,△PBQ的面积为ycm2.
(1)求y与x的函数关系式,写出x的取值范围;
(2)求运动多少秒时,△PBQ的面积为12cm2;
(3)求运动多少秒时,△PBQ的面有最大值.最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.

(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,电线杆上有盏路灯O,小明从点F出发,沿直线FM运动,当他运动2米到达点D处时,测得影长DN=0.6 m,再前进2米到达点B处时,测得影长MB=1.6 m.(图中线段AB、CD、EF表示小明的身高)
(1)请画出路灯O的位置和小明位于F处时,在路灯灯光下的影子;
(2)求小明位于F处的影长.
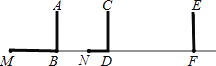
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)写出点![]() 所在直线的函数解析式;
所在直线的函数解析式;
(2)连接![]() ,若线段
,若线段![]() 能构成三角形,求
能构成三角形,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 把四边形
把四边形![]() 的面积分成相等的两部分,试求
的面积分成相等的两部分,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com