
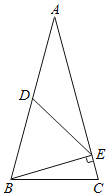
【题目】如图,已知:在△ABC中,∠C=∠ABC,BE⊥AC,△BDE是正三角形.求∠C的度数.
【答案】75°.
【解析】本题首先由等边三角形的性质及垂直定义得到∠DBE=60°,∠BEC=90°,再根据等腰三角形的性质可以得出∠EBC=∠ABC-60°=∠C-60°,最后根据三角形内角和定理得出关系式∠C-60°+∠C=90°解出即可.
解:∵△BDE是正三角形,
∴∠DBE=60°;
∵在△ABC中,∠C=∠ABC,BE⊥AC,
∴∠C=∠ABC=∠ABE+∠EBC则∠EBC=∠ABC﹣60°=∠C﹣60°,∠BEC=90°;
∴∠EBC+∠C=90°,即∠C﹣60°+∠C=90°
解得∠C=75°.
“点睛”本题主要考查等腰三角形的性质及等边三角形的性质及垂直定义,解题的关键是根据三角形内角和定理列出符合题意的简易方程,从而求出结果.


科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
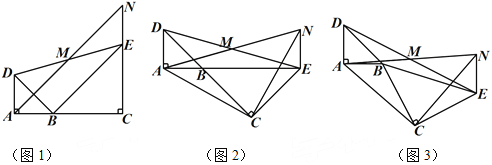
【题目】如图1,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD交于点O,并且∠DAC=60°,∠ADB=15°.点E是AD边上一动点,延长EO交BC于点F.当点E从D点向A点移动过程中(点E与点D,A不重合),则四边形AFCE的变化是( ) 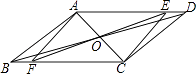
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→菱形→平行四边形→矩形→平行四边形
C.平行四边形→矩形→平行四边形→正方形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
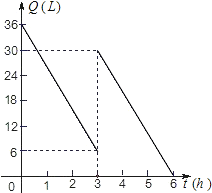
【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。
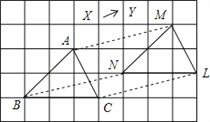
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人在一次买卖中均以120元卖出两件衣服,一件赚20%,一件赔20%,在这次交易中,该商人( )
A.赚10元B.赔10元C.不赚不赔D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com