
 Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ���һ�ǡ�MON����MON=135�㣩������Ϊ�ߣ����ܳ�Ϊ120m��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ������������������Ϊֱ�������Σ�����ڢ�Ϊ���Σ������ı���OBDGΪֱ�����Σ�
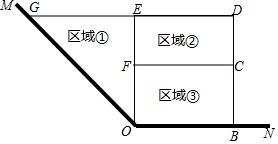
Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ���һ�ǡ�MON����MON=135�㣩������Ϊ�ߣ����ܳ�Ϊ120m��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ������������������Ϊֱ�������Σ�����ڢ�Ϊ���Σ������ı���OBDGΪֱ�����Σ����� ��1������֤��EG=EO=DB��DE=FC=OB����OB=CF=DE=x����GE=OE=BD=$\frac{1}{3}$��120-3x��=40-x���ɢ٢ڢ��������������ȣ��õ�$\frac{1}{2}$��40-x��2=$\frac{1}{2}$•x��40-x�����ⷽ�̼��ɣ�
��2���ٸ���ֱ�����ε������ʽ���㼴�ɣ�����S1��S2��S3=3��2��1���϶�$\frac{1}{2}$��40-x��2=$\frac{1}{2}$��-$\frac{1}{2}$x2+800�����Ƴ�x=$\frac{40}{3}$��40�������������EG=40-$\frac{40}{3}$=$\frac{80}{3}$��ED=$\frac{40}{3}$��DC=$\frac{2}{3}$EG=$\frac{160}{9}$���ɴ˼��ɽ�����⣮
��� �⣺��1���������֪����MON=135�㣬��EOB=��D=��DBO=90�㣬
���EGO=��EOG=45�㣬
��EG=EO=DB��DE=FC=OB����OB=CF=DE=x����GE=OE=BD=$\frac{1}{3}$��120-3x��=40-x��
�ߢ٢ڢ��������������ȣ�
��$\frac{1}{2}$��40-x��2=$\frac{1}{2}$•x��40-x����
��x=20��40����������
��BC=20m��
�ʴ�Ϊ20��
��2����y=$\frac{x+x+40-x}{2}$•��40-x��=-$\frac{1}{2}$x2+800��0��x��40����
�ڡ�S1��S2��S3=3��2��1��
��$\frac{1}{2}$��40-x��2=$\frac{1}{2}$��-$\frac{1}{2}$x2+800����
��x=$\frac{40}{3}$��40����������
��EG=40-$\frac{40}{3}$=$\frac{80}{3}$��ED=$\frac{40}{3}$��DC=$\frac{2}{3}$EG=$\frac{160}{9}$��
��EG��DE��DC=$\frac{80}{3}$��$\frac{40}{3}$��$\frac{160}{9}$=6��3��4��
���� ���⿼��һԪ���η��̵�Ӧ�á������ε������ʽ�����ε����ʡ�ֱ�����ε����ʵ�֪ʶ������Ĺؼ���ѧ�����ò����������̽�����⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
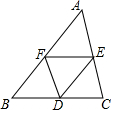 ��ͼ��D��E��F�ǡ�ABC���ߵ��е㣬��DE��AB��DF��AC��EF��BC��ƽ�ơ�AEF���Եõ����������ǣ�������
��ͼ��D��E��F�ǡ�ABC���ߵ��е㣬��DE��AB��DF��AC��EF��BC��ƽ�ơ�AEF���Եõ����������ǣ�������| A�� | ��BDF | B�� | ��DEF | C�� | ��CDE | D�� | ��BDF�͡�CDE |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC�������ڽǵ�ƽ���߽��ڵ�O����D��CA���ӳ����ϣ���DC=BC������BAC=80�㣬���BOD�Ķ���Ϊ100�㣮
��ͼ����֪��ABC�������ڽǵ�ƽ���߽��ڵ�O����D��CA���ӳ����ϣ���DC=BC������BAC=80�㣬���BOD�Ķ���Ϊ100�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����һ������45����������������� | |
| B�� | �����ȱ������� | |
| C�� | ����һ������45�㣬��������3cm���������������� | |
| D�� | ���Ͷ��Ƕ�Ӧ��ȵ��������������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a-3b2��a-2b2=$\frac{1}{a}$ | B�� | ��-$\frac{3x}{4y}$��4=-$\frac{3{x}^{4}}{-4{y}^{3}}$ | ||
| C�� | ��$\frac{2a}{a+c}$��2=$\frac{{a}^{2}}{{c}^{2}}$ | D�� | $\frac{b}{a}$+$\frac{d}{c}$=$\frac{bd}{ac}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com