
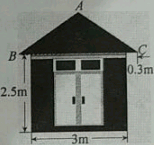
 一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70) 分析 过A作AD⊥BC于D,AD的延长线交地面于E,则DE=2.5m.根据等腰三角形的性质得出BD=DC=$\frac{1}{2}$BC=1.8,利用正切函数的定义求出AD=BD•tan∠ABC≈1.26,则配电房房顶离地面的高度为AD+DE,代入数据计算即可.
解答 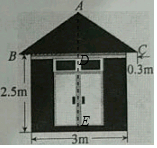 解:如图,过A作AD⊥BC于D,AD的延长线交地面于E,则DE=2.5m.
解:如图,过A作AD⊥BC于D,AD的延长线交地面于E,则DE=2.5m.
∵AB=AC,AD⊥BC,
∴BD=DC=$\frac{1}{2}$BC=$\frac{1}{2}$(3+0.3×2)=1.8,
∵∠ABC=35°,
∴AD=BD•tan∠ABC≈1.8×0.70=1.26,
∴AD+DE≈1.26+2.5≈3.8.
答:配电房房顶离地面的高度约为3.8m.
点评 本题考查了直角三角形的应用,轴对称图形的性质,三角函数的定义.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一垂直于水平地面的灯柱AB被一钢筋CD固定,CD与地面成45°角(∠CDB=45°),在点C上方2m处加固另一条钢筋DE,DE与地面成60°角(∠EDB=60°),则钢筋DE的长度约为多少?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,一垂直于水平地面的灯柱AB被一钢筋CD固定,CD与地面成45°角(∠CDB=45°),在点C上方2m处加固另一条钢筋DE,DE与地面成60°角(∠EDB=60°),则钢筋DE的长度约为多少?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com