
【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC.
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.

【答案】(1)∠C=32°;(2)45°.
【解析】试题分析:连接OB,根据切线的性质,得∠OBA=90°,又∠A=26°,所以∠AOB=64°,再用三角形的外角性质可以求出∠ACB的度数.
(2)由角平分线及三角形外角性质可得∠C+∠CAE=∠FBA+∠BAF,即∠BEF=∠BFE,再利用直径所对的圆周角是直角即可求解.
试题解析:(1)如图:连接OB,
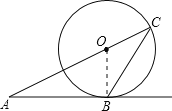
∵AB切⊙O于点B,
∴∠OBA=90°,
∵∠A=26°,
∴∠AOB=90°-26°=64°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=2∠ACB,
∴∠ACB=32°.
(2)如图,连接BD交AE于点F.
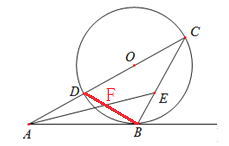
∵AB是⊙O的切线,
∴∠C=∠DBA.
又∵AE是∠CAB的平分线,
∴∠CAE=∠BAE,
∴∠C+∠CAE=∠ABD+∠BAE,
∴∠AEB=∠BFE.
∵CD是⊙O直径,
∴∠CBD=90°.
∴∠AEB=45°.


科目:初中数学 来源: 题型:
【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3. 
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小岛A在港口P的南偏西45°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发.
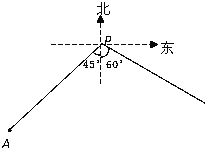
(1)出发后几小时两船与港口P的距离相等;
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);

(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月29日,新建的无锡文化旅游城将盛大开业,开业后预计接待游客量约20 000 000 人次,这个年接待课量可以用科学记数法表示为________人次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知(2x﹣3)7=a0x7+a1x6+a2x5+……+a6x+a7,则a0+a1+a2+……+a7=( )
A. 1B. ﹣1C. 2D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知l1∥l2 , AB∥CD,CE⊥l2 , FG⊥l2 , 下列说法错误的是( ) 
A.l1与l2之间的距离是线段FG的长度
B.CE=FG
C.线段CD的长度就是l1与l2两条平行线间的距离
D.AC=BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com