
分析 (1)根据单项式除以单项式的方法,以及单项式乘单项式的方法,计算(-48a6b5c)÷(24ab4)•(-$\frac{5}{6}$a5b2)即可.
(2)根据xm=3,xn=2,以及幂的乘方与积的乘方的运算方法,求出x2m-3n的值是多少即可.
(3)首先化简代数式(x-3y)2-(x-y)(x+y)-5y2,然后根据6x=5y,求出化简后的算式的值是多少即可.
解答 解:(1)(-48a6b5c)÷(24ab4)•(-$\frac{5}{6}$a5b2)
=-2a5bc•(-$\frac{5}{6}$a5b2)
=$\frac{5}{3}$a10b3c
(2)∵xm=3,xn=2,
∴x2m-3n
=(xm)2÷(xn)3
=32÷23
=$\frac{9}{8}$
(3)(x-3y)2-(x-y)(x+y)-5y2
=x2-6xy+9y2-x2+y2-5y2
=5y2-6xy
=y(5y-6x)
∵6x=5y,
∴原式=y×0=0.
点评 此题主要考查了整式的混合运算-化简求值,要熟练掌握,注意先按运算顺序把整式化简,再把对应字母的值代入求整式的值.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
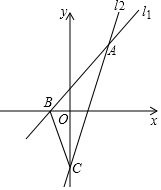 如图,直线l1、l2相交于点A(2,3),直线l1与x轴交点B的坐标为(-1,0),直线l2与y轴交于点C,已知直线l2的解析式为y=2.5x-2,结合图象解答下列问题:
如图,直线l1、l2相交于点A(2,3),直线l1与x轴交点B的坐标为(-1,0),直线l2与y轴交于点C,已知直线l2的解析式为y=2.5x-2,结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
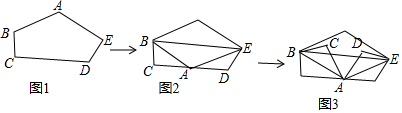
| A. | 56 | B. | 60 | C. | 62 | D. | 68 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
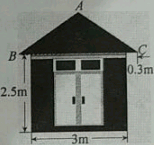 一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com