
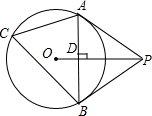
 如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D.
如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D.分析 (1)要证PB为⊙O的切线PB为⊙O的切线,只要证明△OAP≌△OBP即可,根据题目中的条件可以证明该结论成立;
(2)根据同弧所对的圆心角是圆周角的二倍,由tan∠BCA=$\frac{4}{3}$,⊙O的半径为10,可以得到OP和OD的长,从而可以解答本题.
解答  (1)证明:连接OA、OB,如右图所示,
(1)证明:连接OA、OB,如右图所示,
∵PA=PB,OA=OB,OP=OP,
∴△OAP≌△OBP(SSS),
∴∠OAP=∠OBP,
∵PA为⊙O的切线,
∴∠OAP=90°,
∴∠OBP=90°,
∴PB为⊙O的切线;
(2)解:∵△OAP≌△OBP,
∴∠AOP=∠BOP,
又∵∠AOB=2∠BCA=∠AOP+∠BOP,
∴∠BCA=∠AOP,
∵tan∠BCA=$\frac{4}{3}$,⊙O的半径为10,
∴tan∠AOP=$\frac{4}{3}$,OA=10,
∴AP=OA•tan∠AOP=10×$\frac{4}{3}$=$\frac{40}{3}$,OD=6,
∴OP=$\frac{50}{3}$,
∴PD=OP-OD=$\frac{32}{3}$.
点评 本题考查切线的性质、三角形的外接圆与外心、解直角三角形,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源:2017届广东省东莞市堂星晨学校九年级第一次模拟数学试卷(解析版) 题型:单选题
如图,A、D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC等于:
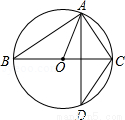
A. 64° B. 58° C. 72° D. 55°
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷(解析版) 题型:解答题
低碳生活备受关注.小明为了了解人们到某超市购物时使用购物袋的情况,利用星期日到该超市对部分购物者进行调查,并把调查结果绘制成两幅不完整的统计图.假设当天每人每次购物时都只用一个环保购物袋(可降解)或塑料购物袋(不可降解).

A.一自备环保购物袋
B.一自备塑料购物袋
C.一购买环保购物袋
D.一购买塑料购物袋
根据以上信息,回答下列问题:
(1)小明这次调查到的购物人数是 人次;
(2)补全两幅统计图;
(3)若当天到该超市购物者共有2000人次,请你估计该天使用环保购物袋有 人次,使用塑料购物袋有 人次;
(4)在大力倡导低碳生活的今天,你认为在购物时应尽量使用 购物袋.(填“环保”或“塑料”)
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷(解析版) 题型:单选题
2015年我市有1.6万名初中毕业生参加升学考试,为了了解这1.6万名考生的数学成绩,从中抽取2000名考生的数学成绩进行统计,在这个问题中样本是( )
A. 1.6万名考生 B. 2000名考生
C. 1.6万名考生的数学成绩 D. 2000名考生的数学成绩
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,如图双曲线y=$\frac{4}{x}$(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=$\frac{2}{x}$(x>0)交于点C,点D,则:
已知,如图双曲线y=$\frac{4}{x}$(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=$\frac{2}{x}$(x>0)交于点C,点D,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<0 | B. | x>0 | C. | x>$\frac{1}{3}$ | D. | x<$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是①③④.(填写序号)
如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是①③④.(填写序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com