
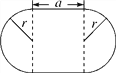
【题目】一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长l;
(2)花坛的面积S;
(3)若a=8m,r=5m,求此时花坛的周长及面积(π取3.14).
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图,线段![]() 、折线
、折线![]() 分别表示两车离甲地的距离
分别表示两车离甲地的距离![]() (单位:千米)与时间
(单位:千米)与时间![]() (单位:小时)之间的函数关系.
(单位:小时)之间的函数关系.
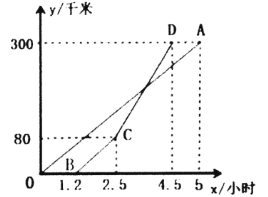
(1)线段![]() 与折线
与折线![]() 中,______(填线段
中,______(填线段![]() 或折线
或折线![]() )表示货车离甲地的距离
)表示货车离甲地的距离![]() 与时间
与时间![]() 之间的函数关系.
之间的函数关系.
(2)求线段![]() 的函数关系式(标出自变量
的函数关系式(标出自变量![]() 取值范围);
取值范围);
(3)货车出发多长时间两车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
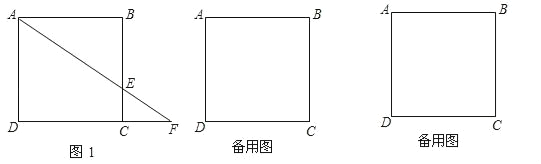
【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“![]() =x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售, 每吨利润为7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨, 如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕.为此,公司研制了三种方案:
方案1:将蔬菜全部进行粗加工;
方案2:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案3:将一部分蔬菜进行精加工, 其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案? 请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A为⊙C上一点,过点A作弦AB,取弦AB上一点P,若满足![]() ≤
≤![]() <1,则称P为点A关于⊙C的黄金点.已知⊙C的半径为3,点A的坐标为(1,0).
<1,则称P为点A关于⊙C的黄金点.已知⊙C的半径为3,点A的坐标为(1,0).
(1)当点C的坐标为(4,0)时,
①在点D(3,0),E(4,1),F(7,0)中,点A关于⊙C的黄金点是 ;
②直线![]() 上存在点A关于⊙C的黄金点P,求点P的横坐标的取值范围;
上存在点A关于⊙C的黄金点P,求点P的横坐标的取值范围;
(2)若y轴上存在点A关于⊙C的黄金点,直接写出点C横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,图①是沿
的中点,图①是沿![]() 将
将![]() 折叠,点
折叠,点![]() 落在
落在![]() 上,图②是绕点
上,图②是绕点![]() 将
将![]() 顺时针旋转
顺时针旋转![]() .
.
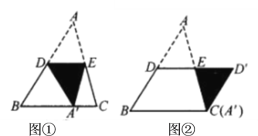
(1)在图①中,判断![]() 和
和![]() 形状.(填空)_______________________________________
形状.(填空)_______________________________________
(2)在图②中,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com