
【题目】在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”图中的P,Q两点即为“等距点”.

(1)已知点A的坐标为![]() .①在点
.①在点![]()
![]()
![]() 中,为点A的“等距点”的是________;②若点B的坐标为
中,为点A的“等距点”的是________;②若点B的坐标为![]() ,且A,B两点为“等距点”,则点B的坐标为________.
,且A,B两点为“等距点”,则点B的坐标为________.
(2)若![]()
![]() 两点为“等距点”,求k的值.
两点为“等距点”,求k的值.
【答案】(1)①E,F. ②![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)①找到E、F、G中到x、y轴距离最大为3的点即可;
②先分析出直线上的点到x、y轴距离中有3的点,再根据“等距点”概念进行解答即可;
(2)先分析出直线上的点到x、y轴距离中有4的点,再根据“等距点”概念进行解答即可.
解:(1)①![]() 点
点![]() 到x,y轴的距离中的最大值为3,
到x,y轴的距离中的最大值为3,
![]() 与点A是“等距点”的点是E,F.
与点A是“等距点”的点是E,F.
②点B坐标中到x,y轴距离中,至少有一个为3的点有![]()
![]()
![]() ,
,
这些点中与点A符合“等距点”的定义的是![]() .
.
故答案为①E,F;②![]() .
.
(2)![]()
![]() 两点为“等距点”.
两点为“等距点”.
若![]() ,则
,则![]() 或
或![]() ,
,
解得![]() (舍去)或
(舍去)或![]() .
.
若![]() 时,则
时,则![]() ,
,
解得![]() (舍去)或
(舍去)或![]() .
.
根据“等距点”的定义知![]() 或
或![]() 符合题意.
符合题意.
即k的值是1或2.


科目:初中数学 来源: 题型:
【题目】一副直角三角板(其中一个三角板的内角是45°,45°,90°,另一个是30°,60°,90°)
(1)如图①放置,AB⊥AD,∠CAE=_______,BC与AD的位置关系是__________;
(2)在(1)的基础上,再拿一个30°,60°,90°的直角三角板,如图②放置,将AC′边和AD边重合, AE是∠CAB′的角平分线吗,如果是,请加以说明,如果不是,请说明理由.
(3)根据(1)(2)的计算,请解决下列问题:
如图③∠BAD=90°,∠BAC=∠FAD= ![]() (
(![]() 是锐角),将一个45°,45°,90°直角三角板的一直角边与AD边重合,锐角顶点A与∠BAD的顶点重合,AE是∠CAF的角平分线吗?如果是,请加以说明,如果不是,请说明理由.
是锐角),将一个45°,45°,90°直角三角板的一直角边与AD边重合,锐角顶点A与∠BAD的顶点重合,AE是∠CAF的角平分线吗?如果是,请加以说明,如果不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,3))、B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为
A. (2,0) B. (2.5,0) C. (4,0), D. (4.5,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求证:无论![]() 为任何实数,抛物线与
为任何实数,抛物线与![]() 轴总有两个交点;
轴总有两个交点;
(2)若A![]() 、B
、B![]() 是抛物线上的两个不同点,求抛物线的表达式和
是抛物线上的两个不同点,求抛物线的表达式和![]() 的值;
的值;
(3)若反比例函数![]() 的图象与(2)中的抛物线在第一象限内的交点的横坐标为
的图象与(2)中的抛物线在第一象限内的交点的横坐标为![]() ,且满足2<
,且满足2<![]() <3,求k的取值范围.
<3,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(-4,0),B(6,0),C(2,4),D(-3,2).
(1)求四边形ABCD的面积;
(2)在y轴上找一点P,使△APB的面积等于四边形的一半,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,
的小数部分我们不可能全部写出来,![]() ,于是可用
,于是可用![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是________,小数部分是________.
的整数部分是________,小数部分是________.
(2)如果![]() 的小数部分为
的小数部分为![]() ,
,![]() 的整数部分为
的整数部分为![]() ,求
,求![]() 的值.
的值.
(3)已知:![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,求
,求![]() 的相反数.
的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016江苏省无锡市)某公司今年如果用原线下销售方式销售一产品,每月的销售额可达100万元.由于该产品供不应求,公司计划于3月份开始全部改为线上销售,这样,预计今年每月的销售额y(万元)与月份x(月)之间的函数关系的图象如图1中的点状图所示(5月及以后每月的销售额都相同),而经销成本p(万元)与销售额y(万元)之间函数关系的图象图2中线段AB所示.

(1)求经销成本p(万元)与销售额y(万元)之间的函数关系式;
(2)分别求该公司3月,4月的利润;
(3)问:把3月作为第一个月开始往后算,最早到第几个月止,该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元?(利润=销售额﹣经销成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
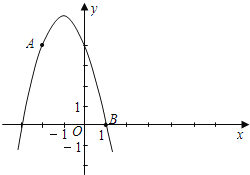
【题目】如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com