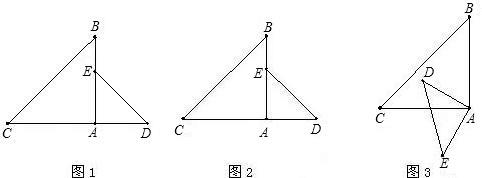
解:(1)在正△ABC中,∠ABC=∠ACB=60°,AB=BC,
∴∠ABE=∠BCD,
∵
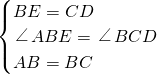
,
∴△ABE≌△BCD,
∴∠E=∠D,
∵∠EBF=∠CBD,
∴∠AFB=∠E+∠EBF=∠D+∠CBD=∠ACB=60°;
(2)在正四边形ABCM中,∠ABC=∠ACB=90°,AB=BC
∴∠ABE=∠BCD,
∵
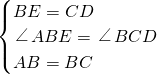
,
∴△ABE≌△BCD,
∴∠E=∠D,
∵∠EBF=∠CBD,
∴∠AFB=∠E+∠EBF=∠D+∠CBD=∠MCB=90°;
(3)在正五边形ABCM中,∠ABC=∠ACB=108°,AB=BC,
∴∠ABE=∠BCD,
∵
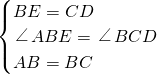
,
∴△ABE≌△BCD,
∴∠E=∠D,
∵∠EBF=∠CBD,
∴∠AFB=∠E+∠EBF=∠D+∠CBD=∠MCB=108°.
故答案为:108°;
(4)结论:∠AFB=∠MCB=
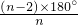
在正n边形ABCM…N中,
∠ABC=∠MCB=
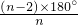
,AB=BC,
∴∠ABE=∠BCD,
∵
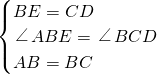
,
∴△ABE≌△BCD,
∴∠E=∠D,
∵∠EBF=∠CBD,
∴∠AFB=∠E+∠EBF=∠D+∠CBD=∠MCB=
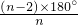
;
(5)由(1)同理即可得出:∠AFB=∠E+∠EBF=∠D+∠CBD=∠MCB=120°.
故答案为:120°.
分析:(1)可通过证三角形AEB和BDC全等得出∠E=∠D,再根据∠EBF=∠CBD,那么这两个三角形的外角∠AFB,∠ACB就应该相等.从而得出∠AFB的度数.
(2)都和(1)相同,都要先证明三角形ABE和BCD全等,然后得出角相等来求解.
(3)都和(1)相同,都要先证明三角形ABE和BCD全等,然后得出角相等来求解.
(4)由正三角形、正四边形、正五边形时,∠AFB的度数分别为60°,90°,108°,可得出“正n边形”,其它条件不变,则∠AFB度数为=
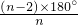
;
(5)都和(1)相同,都要先证明三角形ABE和BCD全等,然后得出角相等来求解.
点评:此题主要考查了正三角边形,正四边形的性质,正五边形的性质与等边三角形与相似三角形的性质以及规律问题应用,利用三角形全等得出角之间关系是解题关键.

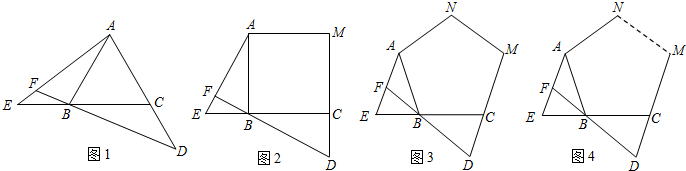
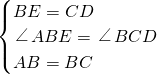 ,
,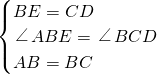 ,
,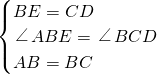 ,
,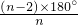 在正n边形ABCM…N中,
在正n边形ABCM…N中,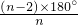 ,AB=BC,
,AB=BC,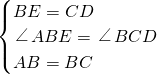 ,
,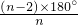 ;
;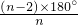 ;
;

 寒假学与练系列答案
寒假学与练系列答案



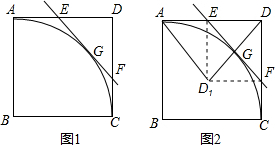 AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.
AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.