
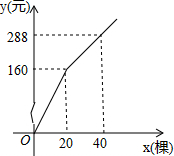
 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.分析 (1)根据函数图象找出点的坐标,结合点的坐标分段利用待定系数法求出函数解析式即可;
(2)根据B种苗的数量不超过35棵,但不少于A种苗的数量可得出关于x的一元一次不等式组,解不等式组求出x的取值范围,再根据“所需费用为W=A种树苗的费用+B种树苗的费用”可得出W关于x的函数关系式,根据一次函数的性质即可解决最值问题.
解答 解:(1)设y与x的函数关系式为:y=kx+b,
当0≤x≤20时,把(0,0),(20,160)代入y=kx+b中,
得:$\left\{\begin{array}{l}{0=b}\\{160=20k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=8}\\{b=0}\end{array}\right.$,
此时y与x的函数关系式为y=8x;
当20≤x时,把(20,160),(40,288)代入y=kx+b中,
得:$\left\{\begin{array}{l}{20k+b=160}\\{40k+b=288}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=6.4}\\{b=32}\end{array}\right.$,
此时y与x的函数关系式为y=6.4x+32.
综上可知:y与x的函数关系式为y=$\left\{\begin{array}{l}{8x(0≤x≤20)}\\{6.4x+32(20≤x≤45)}\end{array}\right.$.
(2)∵B种苗的数量不超过35棵,但不少于A种苗的数量,
∴$\left\{\begin{array}{l}{x≤35}\\{x≥45-x}\end{array}\right.$,
∴22.5≤x≤35,
设总费用为W元,则W=6.4x+32+7(45-x)=-0.6x+347,
∵k=-0.6,
∴y随x的增大而减小,
∴当x=35时,W总费用最低,W最低=-0.6×35+347=326(元).
点评 本题考查了一次函数的应用、待定系数法求函数解析式以及解一元一次不等式组,解题的关键是:(1)分段,利用待定系数法求出函数解析式;(2)根据数量关系找出W关于x的函数关系式.本题属于中档题,难度不大,解决该题型题目时,根据函数图象找出点的坐标,再利用待定系数法求出函数解析式是关键.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=0}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{7x+3=y}\\{8x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{7x-y=3}\\{8x-y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{7x-y=3}\\{8x+2=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{7x+3=y}\\{8x+2=y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com