
 如图,抛物线y=ax2-x-$\frac{3}{2}$与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.求a的值和点E的坐标.
如图,抛物线y=ax2-x-$\frac{3}{2}$与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.求a的值和点E的坐标. 分析 把点A(3,0)代入抛物线y=ax2-x-$\frac{3}{2}$即可求得a的值,正方形OABC可得点C坐标,代入函数解析式求得点D坐标,可知点E横坐标,再利用正方形BDEF的性质得出点E纵坐标问题得解.
解答 解:把点A(3,0)代入抛物线y=ax2-x-$\frac{3}{2}$,
解得a=$\frac{1}{2}$;
∵四边形OABC为正方形,
∴点C的坐标为(0,3),点D的纵坐标为3,
代入y=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
解得x1=1+$\sqrt{10}$,x2=1-$\sqrt{10}$(不合题意,舍去),
因此正方形BDEF的边长B为1+$\sqrt{10}$-3=$\sqrt{10}$-2,
所以AF=3+$\sqrt{10}$-2=1+$\sqrt{10}$,
由此可以得出点E的坐标为(1+$\sqrt{10}$,1+$\sqrt{10}$);
∴a的值为$\frac{1}{2}$和点E的坐标为(1+$\sqrt{10}$,1+$\sqrt{10}$).
点评 此题主要结合图形与图象,关键是利用正方形的性质以及二次函数图象上点的坐标来进行解答.


科目:初中数学 来源: 题型:解答题
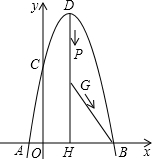 抛物线y=-x2+(2m+3)x+5m+$\frac{5}{2}$与x轴交于A(-1,0),B(x2,0)两点,
抛物线y=-x2+(2m+3)x+5m+$\frac{5}{2}$与x轴交于A(-1,0),B(x2,0)两点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
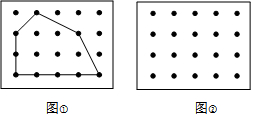 图中有四个相邻点围成正方形面积是一个单位面积.在求图中点阵中多边形的面积时,你可以将多边形分割成若干个小正方形和三角形,分别计算面积后相加;或者你可能想到通过剪拼的方法计算.
图中有四个相邻点围成正方形面积是一个单位面积.在求图中点阵中多边形的面积时,你可以将多边形分割成若干个小正方形和三角形,分别计算面积后相加;或者你可能想到通过剪拼的方法计算.| a | $\frac{1}{2}b$ | S | S,a,b之间 的关系式 | |
| ① | ||||
| ② | 4.5 | |||
| … | … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com