练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下：
    对这两名运动员的成绩进行比较，下列四个结论：
    ①甲运动员得分的极差大于乙运动员得分的极差；
    ②甲运动员得分的中位数大于乙运动员得分的中位数；
    ③甲运动员的得分平均数大于乙运动员的得分平均数；
    ④甲运动员的成绩比乙运动员的成绩稳定．
    其中正确的个数是（　　）
    A．1个B．2个C．3个D．4个

    分析 结合折线统计图，利用数据逐一分析解答即可．

    解答 解：A、由图可知甲、乙运动员第一场比赛得分相同，第十二场比赛得分甲运动员比乙运动员得分高，所以甲运动员得分的极差大于乙运动员得分的极差，故A选项正确；
    B、由图可知甲运动员得分始终大于乙运动员得分，所以甲运动员得分的中位数大于乙运动员得分的中位数，故B选项正确；
    C、由图可知甲运动员得分始终大于乙运动员得分，所以甲运动员的得分平均数大于乙运动员的得分平均数，故C选项正确；
    D、由图可知甲运动员得分数据波动性较大，乙运动员得分数据波动性较小，乙运动员的成绩比甲运动员的成绩稳定，故D选项错误；
    故选C．

    点评 此题主要结合折线统计图，利用极差、中位数、平均数以及方差来进行分析数据，找到解决问题的突破口．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．一种集装箱是正方体形状的，它的体积是64m3，则这种正方体形状的集装箱的边长是4m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

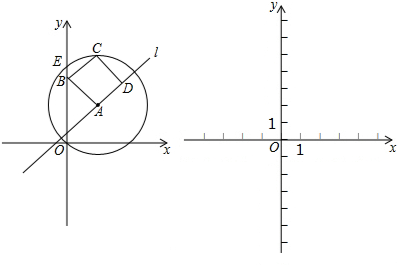
    4．如图，E（2，3），F（3，2）在正方形OABC的边上，⊙D分别切OE，OF于E，F，则⊙D的半径为$\frac{{\sqrt{13}}}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知：如图1，矩形ABCD中，AB=6cm，BC=8cm，点E从点C出发，沿CB方向匀速向点B运动，速度为每秒4cm，同时点P从点A出发，沿AC方向匀速向向点C运动，速度为每秒5cm，过点E平行于BD的直线EF，交CD于F，交AC于Q，当点P运动到线段EF上时，点P、点E都停止运动．设运动时间为t秒，△PEF的面积为y（cm2）
    （1）当t=$\frac{4}{3}$时，点P恰好运动到线段EF上；（请直接写出答案）
    （2）如图2，过点P作PH⊥BC于H，当t为何值时，△PEH∽△EFC？
    （3）求y关于t的函数关系式；
    （4）如图3，取PF的中点N，连接EN，交AC于M，请问随着时间t的改变，点M的位置会发生改变吗？如果会改变请说明点M的变化情况；如果不会改变，请求出点M的具体位置．

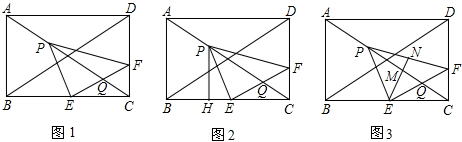
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，在直线l上摆放有△ABC和直角梯形DEFG，且CD=6cm；在△ABC中：∠ACB=90°，∠BAC=30°，AB=4cm；在直角梯形DEFG中：EF∥DG，∠DGF=90°，∠EDG=60°，DG=6cm，DE=4cm．解答下列问题：
    （1）旋转：将△ABC绕点C顺时针方向旋转90°得到对应的△1B1C，求出AB1的长度；
    （2）翻折：将△A1B1C沿过点B1且与l垂直的直线翻折，得到翻折后的对应图形△A2B1C1，试判定四边形A2B1DE的形状？并说明理由；
    （3）平移：将△A2B1C1沿直线l向右平移至△A2B2C2，若设平移的距离为x（0≤x≤8），△A2B2C2与直角梯形重叠部分的面积为y，当y等于△ABC面积的一半时，x的值是多少？

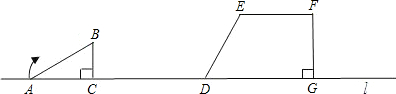
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

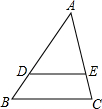    18．如图，△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD：AB=3：4，△ABC的面积为
    16，则四边形DBCE的面积（　　）
    A．9B．12C．4D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

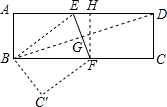    5．如图，矩形ABCD的长AD=9cm，宽AB=3cm，将它折叠，使点D与点B重合，求折叠后DE的长和EF的长分别是（　　）
    A．5cm，3cmB．5cm，$\sqrt{10}$cmC．6cm，$\sqrt{10}$cmD．5cm，4cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在平面直角坐标系xOy中，点A在直线l上，以A为圆心，OA为半径的圆与y轴的另一个交点为E．给出如下定义：若线段OE，⊙A和直线l上分别存在点B，点C和点D，使得四边形ABCD是矩形（点A，B，C，D顺时针排列），则称矩形ABCD为直线l的“理想矩形”．
    例如，下图中的矩形ABCD为直线l的“理想矩形”．
    （1）若点A（-1，2），四边形ABCD为直线x=-1的“理想矩形”，则点D的坐标为（-1，0）；
    （2）若点A（3，4），求直线y=kx+1（k≠0）的“理想矩形”的面积；
    （3）若点A（1，-3），直线l的“理想矩形”面积的最大值为5，此时点D的坐标为（3，-2）或（-1，-2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．先化简，再求代数式（$\frac{1}{x}$+$\frac{x+1}{x}$）÷$\frac{x+2}{{x}^{2}+x}$的值，其中x=cos30°+$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案