
| 3 |
| 2 |
| 2 |

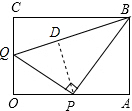 解:(1)△OPQ和△ABP中,∵∠OPQ+∠APB=90°,且∠APB+∠ABP=90°,
解:(1)△OPQ和△ABP中,∵∠OPQ+∠APB=90°,且∠APB+∠ABP=90°,| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 1 |
| 4 |
| 2 |
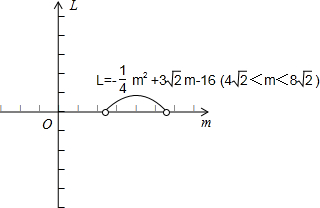 ②设直线BP的解析式为:y=kx+b,代入B(8
②设直线BP的解析式为:y=kx+b,代入B(8| 2 |
| 2 |
|
|
| 2 |
| 2 |
| 1 |
| 4 |
| 2 |
| 2 |
| 1 |
| 4 |
| 2 |
| 1 |
| 4 |
| 2 |
| 2 |
| 2 |
| 1 |
| 4 |
| 2 |
| 1 |
| 4 |
| 2 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,已知:正△OAB的面积为4
如图,已知:正△OAB的面积为4| 3 |
| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 长线交于点E.
长线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分10分)
如图,已知OA⊥OB,OA=8,OB=6,以AB为边作矩形ABCD,使AD=a,过点D作DE垂直OA的延长线交于点E.
(1)求证:△OAB∽△EDA;
(2)当a为何值时,△OAB与△EDA全等?并求出此时点C到OE的距离.

查看答案和解析>>
科目:初中数学 来源:2011届河北省唐山路南数学三模试卷 题型:解答题
(本题满分10分)
如图,已知OA⊥OB,OA=8,OB=6,以AB为边作矩形ABCD,使AD=a,过点D作DE垂直OA的延长线交于点E.
(1)求证:△OAB∽△EDA;
(2)当a为何值时,△OAB与△EDA全等?并求出此时点C到OE的距离.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省启东市九年级中考适应性考试(一模)数学试卷(解析版) 题型:解答题
如图,已知OA⊥OB,OA=4,OB=3,以AB为边作矩形ABCD,使AD= ,过点D作DE垂直OA的延长线且交于点E.(1)求证:△OAB∽△EDA;
,过点D作DE垂直OA的延长线且交于点E.(1)求证:△OAB∽△EDA;

(2)当 为何值时,△OAB与△EDA全等?请说明理由;并求出此时B、D两点的距离.
为何值时,△OAB与△EDA全等?请说明理由;并求出此时B、D两点的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com