
【题目】如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP=4,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.

【答案】(1)4;(2)详见解析
【解析】
(1)首先连接OB,由弦AB⊥OC,劣弧AB的度数为120°,易证得△OBC是等边三角形,则可求得BC的长;
(2)由OC=CP=4,△OBC是等边三角形,可求得BC=CP,即可得∠P=∠CBP,又由等边三角形的性质,∠OBC=60°,∠CBP =30°,则可证得OB⊥BP,继而证得PB是⊙O的切线.
(1)连接OB,
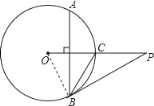
∵弦AB⊥OC,劣弧AB的度数为120°,
∴弧BC与弧AC的度数为:60°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OC=4;
(2)证明:∵OC=CP,BC=OC,
∴BC=CP,
∴∠CBP=∠CPB,
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠CBP=30°,
∴∠OBP=∠CBP+∠OBC=90°,
∴OB⊥BP,
∵点B在⊙O上,
∴PB是⊙O的切线.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知二次函数![]() (a>0)图像与x轴交于点A、B(点A在点B的左侧),与y轴的交于点C,顶点为D .
(a>0)图像与x轴交于点A、B(点A在点B的左侧),与y轴的交于点C,顶点为D .
(1)求点A、B的坐标;
(2)若M为对称轴与x轴交点,且DM=2AM,
①求二次函数解析式;
②当30°<∠ADM<45°时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】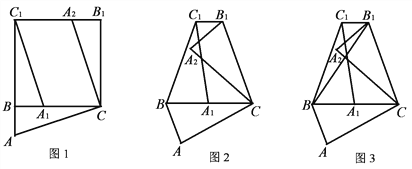
(1)如图1,在Rt△ABC中,∠ABC=90°,以点B为中心,把△ABC逆时针旋转90°,得到△A1BC1;再以点C为中心,把△ABC顺时针旋转90°,得到△A2B1C,连接C1B1,则C1B1与BC的位置关系为_______;
(2)如图2,当△ABC是锐角三角形,∠ABC=α(α≠60°)时,将△ABC按照(1)中的方式旋转α,连接C1B1,探究C1B1与BC的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接B1B,若C1B1=![]() BC,△C1BB1的面积为4,则△B1BC的面积为 .
BC,△C1BB1的面积为4,则△B1BC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
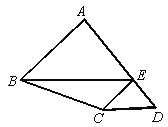
【题目】如图,在四边形ABCD 中,点E在AD上,EC∥AB,EB∥DC,若△ABE面积为5,△ECD的面积为1,则△BCE的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
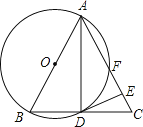
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E.
(1)求证:AD2=ABAE;
(2)若AD=2![]() ,AF=3,求⊙O的半径.
,AF=3,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2015年底拥有家庭轿车64辆,2017年底家庭轿车的拥有量达到100辆.
(1)若该小区2015年底到2018年底家庭轿车拥有量的年平均增长率都相同,求该小区到2018年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作AQ⊥PQ于点Q,连接AP.
(1)填空:抛物线的解析式为 ,点C的坐标 ;
(2)点P在抛物线上运动,若△AQP∽△AOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
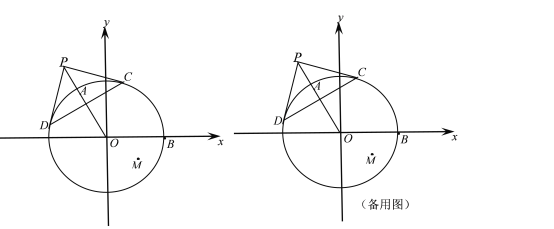
【题目】如图,在平面直角坐标系xoy中,⊙O的圆心O在坐标原点,半径OB在x轴正半轴上,点P是⊙O外一点,连接PO,与⊙O交于点A,PC、PD是⊙O的切线,切点分别为点C、点D,AO=OB=2,∠POB=120°,点M 坐标为(1,-![]() ).
).
(1)求证:OP⊥CD;
(2)连结OM,求∠AOM的大小;
(3) 如果点E在x轴上,且△ABE与△AOM相似,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com