
如图所示,AB是⊙O的一条弦,点C为![]() 的中点,CD是⊙O直径,过C点的直线l交AB所在直线于点E,交⊙O于点F.
的中点,CD是⊙O直径,过C点的直线l交AB所在直线于点E,交⊙O于点F.

(1)判定图中∠CEB与∠FDC大小关系,并写出结论;
(2)将直线l绕C点旋转(与CD不重合),在旋转过程中,E点,F点位置也随之变化,请你在下面的两个备用使(1)结论仍然成立的图形,标相应字母,选其中一个图形给予证明.
|
解答:(1)∠CEB=∠FDC (2)如图
证明:如图(2)∵CD是⊙O的直径,点C是 |
|
名师导引:(1)运用垂径定理和圆周角定理可知CD⊥AB,∠CEB=∠FDC; (2)直线l绕C点旋转:①l过点A,②l过 探究点:动点、动线问题要由条件探索画图,从题目条件及图形性质特征中寻找所探索命题的结论及规律.∠CFD= |


科目:初中数学 来源: 题型:
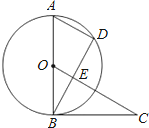 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:
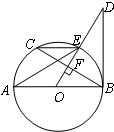 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com