
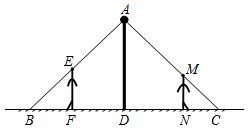
 如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是4m.
如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是4m. 分析 设路灯的高度为xm,根据相似三角形对应边成比例可得,$\frac{EF}{AD}$=$\frac{BF}{BD}$,即$\frac{1.8}{x}$=$\frac{1.8}{1.8+DF}$,可得DF的表达式,再根据相似三角形对应边成比例,同样可得DN的表达式,由于DF+DN=4.7,可得关于x的方程,然后解方程求出x即可.
解答  解:设路灯的高度为xm,
解:设路灯的高度为xm,
∵EF∥AD,
∴△BEF∽△BAD,
∴$\frac{EF}{AD}$=$\frac{BF}{BD}$,
即$\frac{1.8}{x}$=$\frac{1.8}{1.8+DF}$,
解得DF=x-1.8,
∵MN∥AD,
∴△CMN∽△CAD,
∴$\frac{MN}{AD}$=$\frac{CN}{CD}$,
即$\frac{1.5}{x}$=$\frac{1.5}{1.5+DN}$,
解得DN=x-1.5,
∵两人相距4.7m,
∴FD+ND=4.7,
∴x-1.8+x-1.5=4.7,
解得x=4,
故答案为:4m.
点评 本题主要考查了相似三角形的应用以及中心投影,解决问题的关键是掌握:相似三角形的对应边成比例,根据等量关系列出关于x的方程进行求解.解题时注意方程思想的运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图.在正方形ABCD中,点P是BC延长线上一点,BQ⊥PD于点Q,QN⊥BD于点N,连接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,则AN的长为$\sqrt{10}$.
如图.在正方形ABCD中,点P是BC延长线上一点,BQ⊥PD于点Q,QN⊥BD于点N,连接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,则AN的长为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com