
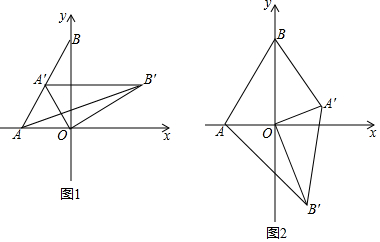
分析 (1)先求出OA,OB,再用锐角三角函数即可得出结论;
(2)根据等边三角形的性质可得AO=AA',再根据直角三角形30°角所对的直角边等于斜边的一半求出AO=$\frac{1}{2}$AB,然后求出AO=OA',再根据等边三角形的性质求出点O到AB的距离等于点A'到AO的距离,然后根据等底等高的三角形的面积相等解答;
(3)方法1、根据旋转的性质可得BO=OB',AA'=OA',再求出∠AON=∠A'OM,然后利用“角角边”证明△AON和△A'OM全等,根据全等三角形对应边相等可得AN=A'M,然后利用等底等高的三角形的面积相等证明.
方法2、利用三角形的中线判断出S△AOB'=S△B'OC,再判断出△A'OB≌△COB',即S△A'OB=S△COB',即可.
解答 解:(1)∵A(-1,0),B(0,$\sqrt{3}$),
∴OA=1,OB=$\sqrt{3}$,
在Rt△AOB中,tan∠BAO=$\frac{OB}{OA}$=$\sqrt{3}$,
∴∠BAO=60°;
(2)∵∠BAO=60°,∠AOB=90°,
∴∠ABO=30°,
∴CA'=AC=$\frac{1}{2}$AB,
∴OA'=AA'=AO,
根据等边三角形的性质可得,△AOA'的边AO、AA'上的高相等,
∴△BA'O的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2,
(3)S1=S2不发生变化;
方法1、理由:如图,过点'作A'M⊥OB.过点A作AN⊥OB'交B'O的延长线于N,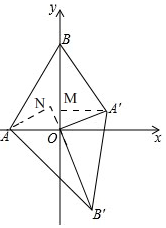 ∵△A'B'O是由△ABO绕点O旋转得到,
∵△A'B'O是由△ABO绕点O旋转得到,
∴BO=OB',AO=OA',
∵∠AON+∠BON=90°,∠A'OM+∠BON=180°-90°=90°,
∴∠AON=∠A'OM,
在△AON和△A'OM中,$\left\{\begin{array}{l}{∠AON=∠A'OM}\\{∠OMA'=∠ONA}\\{AO=A'O}\end{array}\right.$,
∴△AON≌△A'OM(AAS),
∴AN=A'M,
∴△BOA'的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2.
方法2、如图2,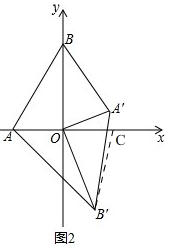
在x轴正半轴上取一点C,使OC=OA,连接B'C,
∴S△AOB'=S△B'OC,
由旋转知,AO'=AO,BO=B'O,
∴OC=OA'
∵∠BOC=∠A'OB'=90°,
∴∠A'OB=∠COB',
∴△A'OB≌△COB',
∴S△A'OB=S△COB',
∴S△A'OB=S△AOB',
即S1=S2
点评 此题是几何变换综合题,主要考查了全等三角形的判定与性质,锐角三角函数,三角形的面积计算公式,等边三角形的判定与性质,直角三角形30°角所对的直角边等于斜边的一半的性质的综合应用,熟练掌握等底等高的三角形的面积相等,以及全等三角形的面积相等是解题的关键.


科目:初中数学 来源: 题型:解答题
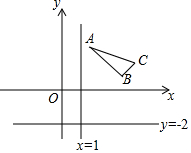 如图,△ABC的顶点分别为A(2,3),B(4,1),C(5,2),分别作出△ABC关于直线x=1对称的图形△A1B1C1和关于直线y=-2对称的图形△A2B2C2.
如图,△ABC的顶点分别为A(2,3),B(4,1),C(5,2),分别作出△ABC关于直线x=1对称的图形△A1B1C1和关于直线y=-2对称的图形△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
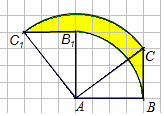 如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1,若网格小正方形的边长为1cm,则线段BC所扫过的图形(阴影部分)的面积为$\frac{9π}{4}$(结果保留π).
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1,若网格小正方形的边长为1cm,则线段BC所扫过的图形(阴影部分)的面积为$\frac{9π}{4}$(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
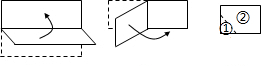
| A. | 直角三角形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{1}{27}$ | D. | -$\frac{1}{27}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
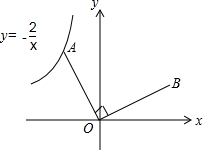 如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.
如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com