
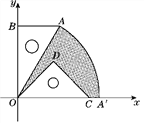
ĄŸÌâÄżĄżÈçÍŒŁŹÓĐÒ»żéșŹ30ĄăœÇ”ÄÖ±œÇÈęœÇ°ćOAB”ÄÖ±œÇ±ßBO”Äł€ÇĄÓëÁíÒ»żé”ÈŃüÖ±œÇÈęœÇ°ćODC”Äб±ßOC”Äł€Ïà”ÈŁŹ°ŃŐâÁœżéÈęœÇ°ć·ĆÖĂÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÇÒOBŁœ3![]() .
.
(1)ÈôÄł·Ž±ÈÀęșŻÊę”ÄÍŒÏó”ÄÒ»žö·Ö֧ǥșĂŸčę”ăAŁŹÇóŐâžö·Ž±ÈÀęșŻÊę”ÄœâÎöÊœŁ»
(2)Èô°ŃșŹ30ĄăœÇ”ÄÖ±œÇÈęœÇ°ćÈÆ”ăO°ŽËłÊ±Őë·œÏòĐęŚȘșóŁŹĐ±±ßOAÇĄșĂÂäÔÚxÖáÉÏŁŹ”ăAÂäÔÚ”ăAĄäŽŠŁŹÊÔÇóÍŒÖĐÒőÓ°Čż·Ö”ÄĂæ»ęŁź(œáčû±ŁÁôŠĐ)
ĄŸŽđ°žĄż(1)·Ž±ÈÀęșŻÊę”ÄœâÎöÊœÎȘyŁœ![]() Ł»(2)SÒőÓ°Łœ6ŠĐŁ
Ł»(2)SÒőÓ°Łœ6ŠĐŁ![]() .
.
ĄŸœâÎöĄż·ÖÎöŁșŁš1Ł©žùŸĘtan30Ąă=![]() ŁŹÇółöABŁŹœű¶űÇółöOAŁŹ”ĂłöA”ÄŚű±êŁŹÉèčęA”ÄË«ÇúÏߔĜâÎöÊœÊÇy=
ŁŹÇółöABŁŹœű¶űÇółöOAŁŹ”ĂłöA”ÄŚű±êŁŹÉèčęA”ÄË«ÇúÏߔĜâÎöÊœÊÇy=![]() ŁŹ°ŃA”ÄŚű±êŽúÈëÇółöŒŽżÉŁ»Łš2Ł©ÇółöĄÏAOAĄäŁŹžùŸĘÉÈĐΔÄĂæ»ęč«ÊœÇółöÉÈĐÎAOAĄä”ÄĂæ»ęŁŹÇółöODĄąDCł€ŁŹÇółöĄśODC”ÄĂæ»ęŁŹÏàŒőŒŽżÉÇółöŽđ°žŁź
ŁŹ°ŃA”ÄŚű±êŽúÈëÇółöŒŽżÉŁ»Łš2Ł©ÇółöĄÏAOAĄäŁŹžùŸĘÉÈĐΔÄĂæ»ęč«ÊœÇółöÉÈĐÎAOAĄä”ÄĂæ»ęŁŹÇółöODĄąDCł€ŁŹÇółöĄśODC”ÄĂæ»ęŁŹÏàŒőŒŽżÉÇółöŽđ°žŁź
±ŸÌâœâÎöŁș
(1)ÔÚRtĄśOBAÖĐŁŹĄÏAOBŁœ30ĄăŁŹOBŁœ3![]() ŁŹ
ŁŹ
ĄàABŁœOBĄ€tan 30ĄăŁœ3.
Ąà”ăA”ÄŚű±êÎȘ(3ŁŹ3![]() )Łź
)Łź
Éè·Ž±ÈÀęșŻÊę”ÄœâÎöÊœÎȘyŁœ![]() (kĄÙ0)ŁŹ
(kĄÙ0)ŁŹ
Ąà3![]() Łœ
Łœ![]() ŁŹĄàkŁœ9
ŁŹĄàkŁœ9![]() ŁŹÔòŐâžö·Ž±ÈÀęșŻÊę”ÄœâÎöÊœÎȘyŁœ
ŁŹÔòŐâžö·Ž±ÈÀęșŻÊę”ÄœâÎöÊœÎȘyŁœ![]() .
.
(2)ÔÚRtĄśOBAÖĐŁŹĄÏAOBŁœ30ĄăŁŹABŁœ3ŁŹ
sin ĄÏAOBŁœ![]() ŁŹŒŽsin 30ĄăŁœ
ŁŹŒŽsin 30ĄăŁœ![]() ŁŹ
ŁŹ
ĄàOAŁœ6.
ÓÉÌâÒâ”ĂŁșĄÏAOCŁœ60ĄăŁŹSÉÈĐÎAOAĄäŁœ![]() Łœ6ŠĐ.
Łœ6ŠĐ.
ÔÚRtĄśOCDÖĐŁŹĄÏDOCŁœ45ĄăŁŹOCŁœOBŁœ3![]() ŁŹ
ŁŹ
ĄàODŁœOCĄ€cos 45ĄăŁœ3![]() ĄÁ
ĄÁ![]() Łœ
Łœ![]() .
.
ĄàSĄśODCŁœ![]() OD2Łœ
OD2Łœ![]()
![]() Łœ
Łœ![]() .
.
ĄàSÒőÓ°ŁœSÉÈĐÎAOAĄäŁSĄśODCŁœ6ŠĐŁ![]() .
.
”ăŸŠŁș±ŸÌâżŒČéÁËčŽčɶšÀíĄąŽę¶šÏ”Êę·šÇóșŻÊęœâÎöÊœĄąÌŰÊâœÇ”ÄÈęœÇșŻÊęÖ”ĄąÉÈĐΔÄĂæ»ęŒ°”ÈŃüÈęœÇĐΔÄĐÔÖÊŁŹ±ŸÌâÊôÓÚÖĐ””Ì⣏ÄѶÈČ»ŽóŁŹœ«Č»čæÔò”ÄÍŒĐΔÄĂæ»ę±íÊŸłÉ¶àžöčæÔòÍŒĐΔÄĂæ»ęÖźșÍÊÇœâŽđ±ŸÌâ”ÄčŰŒü.
ĄŸÌâĐÍĄżœâŽđÌâ
ĄŸœáÊűĄż
26
ĄŸÌâÄżĄżŸŰĐÎABCDÒ»Ìő±ßADŁœ8ŁŹœ«ŸŰĐÎABCDŐÛ”țŁŹÊč”Ă”ăBÂäÔÚCD±ßÉϔĔăPŽŠŁź
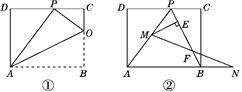
(1)ÈçÍŒąÙŁŹÒŃÖȘŐÛșÛÓë±ßBCœ»ÓÚ”ăOŁŹÁŹœÓAPŁŹOPŁŹOA.
ąÙ ÇóÖ€ŁșĄśOCPĄŚĄśPDAŁ»
ąÚ ÈôĄśOCPÓ륜PDA”ÄĂæ»ę±ÈÎȘ1:4ŁŹÇó±ßAB”Äł€Łź
(2)ÈçÍŒąÚŁŹÔÚ(1)”ÄÌőŒțÏÂŁŹČÁÈ„AOșÍOPŁŹÁŹœÓBP.¶Ż”ăMÔÚÏ߶ÎAPÉÏ(Č»Óë”ăPŁŹAÖŰșÏ)ŁŹ¶Ż”ăNÔÚÏ߶ÎAB”ÄŃÓł€ÏßÉÏŁŹÇÒBNŁœPMŁŹÁŹœÓMNœ»PBÓÚ”ăFŁŹŚśMEĄÍBPÓÚ”ăE.ÊÔÎʶŻ”ăMŁŹNÔÚÒƶŻ”ÄčęłÌÖĐŁŹÏ߶ÎEF”Äł€¶ÈÊÇ·ń·ąÉú±ä»ŻŁżÈôČ»±äŁŹÇółöÏ߶ÎEF”Äł€¶ÈŁ»Èô±ä»ŻŁŹË”ĂśÀíÓÉŁź
ĄŸŽđ°žĄż(1)ąÙրÜŒûœâÎöŁ»ąÚABŁœ10Ł» (2)ÔÚ(1)”ÄÌőŒțÏÂŁŹ”ăMŁŹNÔÚÒƶŻ”ÄčęłÌÖĐŁŹÏ߶ÎEF”Äł€¶ÈČ»±äŁŹËü”Äł€¶ÈșăÎȘ2![]() .
.
ĄŸœâÎöĄżÊÔÌâ·ÖÎöŁșŁš1Ł©ÏÈÖ€łöĄÏC=ĄÏD=90ĄăŁŹÔÙžùŸĘĄÏ1+ĄÏ3=90ĄăŁŹĄÏ1+ĄÏ2=90ĄăŁŹ”ĂłöĄÏ2=ĄÏ3ŁŹŒŽżÉÖ€łöĄśOCPĄŚĄśPDAŁ»žùŸĘĄśOCPÓ륜PDA”ÄĂæ»ę±ÈÎȘ1Łș4ŁŹ”ĂłöCP=![]() AD=4ŁŹÉèOP=xŁŹÔòCO=8©xŁŹÓÉčŽčɶšÀí”ĂÁĐ·œłÌŁŹÇółöxŁŹŚîșóžùŸĘCD=AB=2OPŒŽżÉÇółö±ßCD”Äł€Ł»
AD=4ŁŹÉèOP=xŁŹÔòCO=8©xŁŹÓÉčŽčɶšÀí”ĂÁĐ·œłÌŁŹÇółöxŁŹŚîșóžùŸĘCD=AB=2OPŒŽżÉÇółö±ßCD”Äł€Ł»
Łš2Ł©ŚśMQĄÎANŁŹœ»PBÓÚ”ăQŁŹÇółöMP=MQŁŹBN=QMŁŹ”ĂłöMP=MQŁŹžùŸĘMEĄÍPQŁŹ”ĂłöEQ=![]() PQŁŹžùŸĘĄÏQMF=ĄÏBNFŁŹÖ€łöĄśMFQĄŐĄśNFBŁŹ”ĂłöQF=
PQŁŹžùŸĘĄÏQMF=ĄÏBNFŁŹÖ€łöĄśMFQĄŐĄśNFBŁŹ”ĂłöQF=![]() QBŁŹÔÙÇółöEF=
QBŁŹÔÙÇółöEF=![]() PBŁŹÓÉŁš1Ł©ÖĐ”ÄœáÂÛÇółöPB”Äł€ŁŹŚîșóŽúÈëEF=
PBŁŹÓÉŁš1Ł©ÖĐ”ÄœáÂÛÇółöPB”Äł€ŁŹŚîșóŽúÈëEF=![]() PBŒŽżÉ”ĂłöÏ߶ÎEF”Äł€¶ÈČ»±äŁź
PBŒŽżÉ”ĂłöÏ߶ÎEF”Äł€¶ÈČ»±äŁź
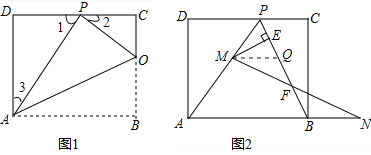
ÊÔÌâœâÎöŁșŁš1Ł©ÈçÍŒ1ŁŹĄßËıßĐÎABCDÊÇŸŰĐÎŁŹĄàĄÏC=ĄÏD=90ĄăŁŹĄàĄÏ1+ĄÏ3=90ĄăŁŹĄßÓÉŐÛ”țżÉ”ĂĄÏAPO=ĄÏB=90ĄăŁŹĄàĄÏ1+ĄÏ2=90ĄăŁŹĄàĄÏ2=ĄÏ3ŁŹÓ֥ߥÏD=ĄÏCŁŹĄàĄśOCPĄŚĄśPDAŁ»ĄßĄśOCPÓ륜PDA”ÄĂæ»ę±ÈÎȘ1Łș4ŁŹĄà![]() =
=![]() ŁŹĄàCP=
ŁŹĄàCP=![]() AD=4ŁŹÉèOP=xŁŹÔòCO=8©xŁŹÔÚRtĄśPCOÖĐŁŹĄÏC=90ĄăŁŹÓÉčŽčɶšÀí”Ă Łș
AD=4ŁŹÉèOP=xŁŹÔòCO=8©xŁŹÔÚRtĄśPCOÖĐŁŹĄÏC=90ĄăŁŹÓÉčŽčɶšÀí”Ă Łș ![]() ŁŹœâ”ĂŁșx=5ŁŹĄàCD=AB=AP=2OP=10ŁŹĄà±ßCD”Äł€ÎȘ10Ł»
ŁŹœâ”ĂŁșx=5ŁŹĄàCD=AB=AP=2OP=10ŁŹĄà±ßCD”Äł€ÎȘ10Ł»
Łš2Ł©ŚśMQĄÎANŁŹœ»PBÓÚ”ăQŁŹÈçÍŒ2ŁŹĄßAP=ABŁŹMQĄÎANŁŹĄàĄÏAPB=ĄÏABP=ĄÏMQPŁŹĄàMP=MQŁŹĄßBN=PMŁŹĄàBN=QMŁźĄßMP=MQŁŹMEĄÍPQŁŹĄàEQ=![]() PQŁźĄßMQĄÎANŁŹĄàĄÏQMF=ĄÏBNFŁŹÔÚĄśMFQșÍĄśNFBÖĐŁŹĄßĄÏQFM=ĄÏNFBŁŹĄÏQMF=ĄÏBNFŁŹMQ=BNŁŹĄàĄśMFQĄŐĄśNFBŁšAASŁ©ŁŹĄàQF=
PQŁźĄßMQĄÎANŁŹĄàĄÏQMF=ĄÏBNFŁŹÔÚĄśMFQșÍĄśNFBÖĐŁŹĄßĄÏQFM=ĄÏNFBŁŹĄÏQMF=ĄÏBNFŁŹMQ=BNŁŹĄàĄśMFQĄŐĄśNFBŁšAASŁ©ŁŹĄàQF=![]() QBŁŹĄàEF=EQ+QF=
QBŁŹĄàEF=EQ+QF=![]() PQ+
PQ+![]() QB=
QB=![]() PBŁŹÓÉŁš1Ł©ÖĐ”ÄœáÂÛżÉ”ĂŁșPC=4ŁŹBC=8ŁŹĄÏC=90ĄăŁŹĄàPB=
PBŁŹÓÉŁš1Ł©ÖĐ”ÄœáÂÛżÉ”ĂŁșPC=4ŁŹBC=8ŁŹĄÏC=90ĄăŁŹĄàPB=![]() =
=![]() ŁŹĄàEF=
ŁŹĄàEF=![]() PB=
PB=![]() ŁŹĄàÔÚŁš1Ł©”ÄÌőŒțÏÂŁŹ”±”ăMĄąNÔÚÒƶŻčęłÌÖĐŁŹÏ߶ÎEF”Äł€¶ÈČ»±äŁŹËü”Äł€¶ÈÎȘ
ŁŹĄàÔÚŁš1Ł©”ÄÌőŒțÏÂŁŹ”±”ăMĄąNÔÚÒƶŻčęłÌÖĐŁŹÏ߶ÎEF”Äł€¶ÈČ»±äŁŹËü”Äł€¶ÈÎȘ![]() Łź
Łź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
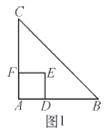
ĄŸÌâÄżĄżÈçÍŒ1ŁŹĄśABCÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁŹËıßĐÎADEFÊÇŐę·œĐÎŁŹ”ăDĄąF·Ö±đÔÚABĄąAC±ßÉÏŁŹŽËʱBD=CFŁŹBDĄÍCFłÉÁą.
(1)”±Őę·œĐÎADEFÈÆ”ăAÄæʱŐëĐęŚȘŠÈ(0Ąă<ŠÈ<90Ąă)ʱŁŹÈçÍŒ2ŁŹBD=CFłÉÁąÂđŁżÈôłÉÁąŁŹÇëրÜŁ»ÈôČ»łÉÁąŁŹÇë˔ÜÀíÓÉ.
(2)”±Őę·œĐÎADEFÈÆ”ăAÄæʱŐëĐęŚȘ45ĄăʱŁŹÈçÍŒ3ŁŹŃÓł€BDœ»CFÓÚ”ăG.
ąÙÇóÖ€ŁșBDĄÍCFŁ» ąÚ”±AB=4ŁŹAD=![]() ʱŁŹÇóÏ߶ÎBG”Äł€.
ʱŁŹÇóÏ߶ÎBG”Äł€.


Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
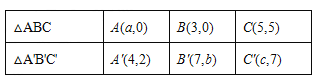
ĄŸÌâÄżĄżÒŃÖȘĄśA'B'C'ÊÇÓÉĄśABCŸčęÆœÒÆ”Ă”œ”Ä,ËüĂǔĶ„”ăÔÚÆœĂæÖ±œÇŚű±êÏ”ÖДČű±êÈçϱíËùÊŸ:
(1)čÛČì±íÖĐžś¶ÔÓŠ”ăŚű±ê”ı仯,ČąÌîżŐ:
a= , b= ,c= ;
(2)ÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐ»łöĄśABCŒ°ÆœÒÆșó”ÄĄśA'B'C';(3)ĄśA'B'C'”ÄĂæ»ęÊÇ .
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒ»ŽÎșŻÊęyŁœ©![]() x+4”ÄÍŒÏó·Ö±đÓëxÖᣏyÖá”ÄŐę°ëÖ᜻ÓÚ”ăEĄąFŁŹÒ»ŽÎșŻÊęyŁœkx©4”ÄÍŒÏóÓëÖ±ÏßEFœ»ÓÚ”ăAŁšmŁŹ2Ł©ŁŹÇÒœ»ÓÚxÖáÓÚ”ăPŁŹ
x+4”ÄÍŒÏó·Ö±đÓëxÖᣏyÖá”ÄŐę°ëÖ᜻ÓÚ”ăEĄąFŁŹÒ»ŽÎșŻÊęyŁœkx©4”ÄÍŒÏóÓëÖ±ÏßEFœ»ÓÚ”ăAŁšmŁŹ2Ł©ŁŹÇÒœ»ÓÚxÖáÓÚ”ăPŁŹ
Łš1Ł©Çóm”ÄÖ”Œ°”ăEĄąF”ÄŚű±êŁ»
Łš2Ł©ÇóĄśAPE”ÄĂæ»ęŁ»
Łš3Ł©ÈôB”ăÊÇxÖáÉϔĶŻ”㣏ÎÊÔÚÖ±ÏßEFÉÏŁŹÊÇ·ńŽæÔÚ”ăQŁšQÓëAČ»ÖŰșÏŁ©ŁŹÊ襜BEQÓ륜APEÈ«”ÈŁżÈôŽæÔÚŁŹÇëÇółö”ăQ”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹ”ăAŁŹBŁŹC±íÊŸÄłÂĂÓΟ°ÇűÈęžöÀÂł”ŐŸ”ÄλÖĂŁŹÏ߶ÎABŁŹBC±íÊŸÁŹœÓÀÂł”ŐŸ”ÄžÖÀÂŁŹÒŃÖȘAŁŹBŁŹCÈę”ăÔÚÍŹÒ»ÇŠÖ±ÆœĂæÄÚŁŹËüĂÇ”ÄșŁ°Îžß¶ÈAAĄäŁŹBBĄäŁŹCCĄä·Ö±đÎȘ110ĂŚŁŹ310ĂŚŁŹ710ĂŚŁŹžÖÀÂAB”ÄƶÈi1Łœ1ĄĂ2ŁŹžÖÀÂBC”ÄƶÈi2Łœ1ĄĂ1ŁŹŸ°ÇűÒòžÄÔìÀÂł”Ïß·ŁŹĐèÒȘŽÓA”œCÖ±ÏߌÜÉèÒ»ÌőžÖÀÂŁŹÄÇĂŽžÖÀÂAC”Äł€¶ÈÊǶàÉÙĂŚŁż(ŚąŁșƶÈiÊÇÖžÆÂĂæ”ÄÇŠÖ±žß¶ÈÓëËźÆœżí¶È”ıÈ)

ĄŸŽđ°žĄżžÖÀÂAC”Äł€¶ÈÎȘ1 000ĂŚŁź
ĄŸœâÎöĄżÊÔÌâ·ÖÎöŁșčę”ăAŚśAEĄÍCCĄäÓÚ”ăEŁŹœ»BBĄäÓÚ”ăFŁŹčę”ăBŚśBDĄÍCCĄäÓÚ”ăDŁŹ·Ö±đÇółöAEĄąCEŁŹÀûÓĂčŽčɶšÀíÇóœâACŒŽżÉŁź
ÊÔÌâœâÎöŁșčę”ăAŚśAEĄÍCCĄäÓÚ”ăEŁŹœ»BBĄäÓÚ”ăFŁŹčę”ăBŚśBDĄÍCCĄäÓÚ”ăDŁŹ
ÔòĄśAFBĄąĄśBDCĄąĄśAEC¶ŒÊÇÖ±œÇÈęœÇĐÎŁŹËıßĐÎAAĄäBĄäFŁŹBBĄäCĄäDșÍBFED¶ŒÊÇŸŰĐÎŁŹ
ĄàBF=BBĄä-BĄäF=BBĄä-AAĄä=310-110=200ŁŹ
CD=CCĄä-CĄäD=CCĄä-BBĄä=710-310=400ŁŹ
Ąßi1=1Łș2ŁŹi2=1Łș1ŁŹ
ĄàAF=2BF=400ŁŹBD=CD=400ŁŹ
ÓÖĄßEF=BD=400ŁŹDE=BF=200ŁŹ
ĄàAE=AF+EF=800ŁŹCE=CD+DE=600ŁŹ
ĄàÔÚRtĄśAECÖĐŁŹAC=![]() ŁšĂŚŁ©Łź
ŁšĂŚŁ©Łź
ŽđŁșžÖÀÂAC”Äł€¶ÈÊÇ1000ĂŚŁź
żŒ”ăŁșœâÖ±œÇÈęœÇĐΔÄÓŠÓĂ-ƶÈÆÂœÇÎÊÌ⣟
ĄŸÌâĐÍĄżœâŽđÌâ
ĄŸœáÊűĄż
24
ĄŸÌâÄżĄżÈçÍŒąÙŁŹABÎȘ°ëÔČ”ÄÖ±Ÿ¶ŁŹOÎȘÔČĐÄŁŹCÎȘÔČ»ĄÉÏÒ»”㣏ADŽčÖ±ÓÚčęC”ă”ÄÇĐÏߣŹŽčŚăÎȘDŁŹAB”ÄŃÓł€Ïßœ»Ö±ÏßCDÓÚ”ăE.
(1)ÇóÖ€ŁșACÆœ·ÖĄÏDABŁ»
(2)ÈôABŁœ4ŁŹBÎȘOE”ÄÖД㣏CFĄÍABŁŹŽčŚăÎȘ”ăFŁŹÇóCF”Äł€Ł»
(3)ÈçÍŒąÚŁŹÁŹœÓODœ»ACÓÚ”ăGŁŹÈô![]() ŁŹÇósinE”ÄÖ”Łź
ŁŹÇósinE”ÄÖ”Łź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒ»ËÒșËDZͧÔÚșŁĂæDFÏÂ600ĂŚA”㎊Čâ”Ăž©œÇÎȘ30ĄăŐęÇ°·œ”ÄșŁ”ŚC”㎊ÓĐșÚÏ»ŚÓŁŹŒÌĐűÔÚÍŹÒ»Éî¶ÈÖ±ÏßșœĐĐ2000ĂŚ”œB”㎊Čâ”ĂŐęÇ°·œC”㎊”Äž©œÇÎȘ45ĄăŁźÇóșŁ”ŚC”㎊ŸàÀëșŁĂæDF”ÄÉî¶ÈŁšœáčû±ŁÁôžùșĆŁ©

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹABCD”ĶԜÇÏßACĄąBDœ»ÓÚ”ăOŁŹAEÆœ·ÖĄÏBADœ»BCÓÚ”ăEŁŹÇÒĄÏADC=60ĄăŁŹAB=![]() BCŁŹÁŹœÓOEŁźÏÂÁĐœáÂÛŁșąÙĄÏCAD=30ĄăŁ»ąÚSABCD=ABACŁ»ąÛOB=ABŁ»ąÜOE=
BCŁŹÁŹœÓOEŁźÏÂÁĐœáÂÛŁșąÙĄÏCAD=30ĄăŁ»ąÚSABCD=ABACŁ»ąÛOB=ABŁ»ąÜOE=![]() BCŁŹłÉÁą”ÄžöÊęÓĐŁšĄĄĄĄŁ©
BCŁŹłÉÁą”ÄžöÊęÓĐŁšĄĄĄĄŁ©

A. 1žö B. 2žö C. 3žö D. 4žö
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżĄŸÎÊÌâÇéŸłĄż
ÈçÍŒ1ŁŹËıßĐÎABCDÊÇŐę·œĐÎŁŹMÊÇBC±ßÉÏ”ÄÒ»”㣏EÊÇCD±ß”ÄÖД㣏AEÆœ·ÖĄÏDAMŁź

ĄŸÌœŸżŐčÊŸĄż
Łš1Ł©Ö€ĂśŁșAM=AD+MCŁ»
Łš2Ł©AM=DE+BMÊÇ·ńłÉÁąŁżÈôłÉÁąŁŹÇëžűłöրÜŁ»ÈôČ»łÉÁąŁŹÇë˔ÜÀíÓÉŁź
ĄŸÍŰŐčŃÓÉìĄż
Łš3Ł©ÈôËıßĐÎABCDÊÇł€ÓëżíČ»Ïà”ȔğŰĐÎŁŹÆäËûÌőŒțČ»±äŁŹÈçÍŒ2ŁŹÌœŸżŐčÊŸŁš1Ł©ĄąŁš2Ł©ÖĐ”ÄœáÂÛÊÇ·ńłÉÁąŁżÇë·Ö±đŚśłöĆĐ¶ÏŁŹČ»ĐèÒȘրÜŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŃ§Ï°Ą°ÀûÓĂÈęœÇșŻÊęČâžßĄ±șóŁŹÄłŚÛșÏÊ”Œù»î¶ŻĐĄŚéÊ””ŰČâÁżÁË·ï»ËÉœÓëÖĐĐÄč㳥”ÄÏà¶Ôžß¶ÈABŁŹÆäČâÁżČœÖèÈçÏÂŁș
Łš1Ł©ÔÚÖĐĐÄč㳥Čâ”ăCŽŠ°ČÖĂČâÇăÆśŁŹČâ”ĂŽËʱɜ¶„A”ÄŃöœÇĄÏAFH=30ĄăŁ»
Łš2Ł©ÔÚČâ”ăCÓëÉœœĆBÖźŒä”ÄDŽŠ°ČÖĂČâÇăÆśŁšCĄąDÓëBÔÚÍŹÒ»Ö±ÏßÉÏŁŹÇÒCĄąDÖźŒä”ÄŸàÀëżÉÒÔÖ±œÓČâ”ĂŁ©ŁŹČâ”ĂŽËʱɜ¶„ÉÏșìŸüÍ€¶„ČżE”ÄŃöœÇĄÏEGH=45ĄăŁ»
Łš3Ł©Čâ”ĂČâÇăÆś”Ğ߶ÈCF=DG=1.5ĂŚŁŹČąČâ”ĂCDÖźŒä”ÄŸàÀëÎȘ288ĂŚŁ»
ÒŃÖȘșìŸüÍ€žß¶ÈÎȘ12ĂŚŁŹÇëžùŸĘČâÁżÊęŸĘÇółö·ï»ËÉœÓëÖĐĐÄč㳥”ÄÏà¶Ôžß¶ÈABŁźŁš![]() ÈĄ1.732ŁŹœáčû±ŁÁôŐûÊ꣩
ÈĄ1.732ŁŹœáčû±ŁÁôŐûÊ꣩

Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com