
【题目】如图,抛物线y=ax2+bx﹣2交x轴负半轴于点A(﹣1,0),与y轴交于B点.过B点的直线l交抛物线于点C(3,﹣1).过点C作CD⊥x轴,垂足为D.点P为x轴正半轴上的动点,过P点作x轴的垂线,交直线l于点E,交抛物线于点F.设P点的横坐标为t.
(1)求抛物线的解析式;
(2)连接OE,求△POE面积的最大值;
(3)连接DE,CF,是否存在这样的t值:以点C,D,E,F为顶点的四边形是平行四边形?请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在这样的t值:以点C,D,E,F为顶点的四边形是平行四边形.
;(3)存在这样的t值:以点C,D,E,F为顶点的四边形是平行四边形.
【解析】
1)将点A、C的坐标代入函数解析式,利用解方程组求得系数的值即可;
(2)根据三角形的面积公式,函数图象上点的坐标特征求得S△POE=![]() t(
t(![]() t-2)=
t-2)=![]() (t-3)2-
(t-3)2-![]() ,所以由二次函数的性质求得答案;
,所以由二次函数的性质求得答案;
(3)根据平行四边形的对边相等的性质和坐标与图形的性质求得答案.
(1)把A(﹣1,0),C(3,﹣1)代入y=ax2+bx﹣2,得
![]() .
.
解得 .
.
则该抛物线的解析式为![]() ;
;
(2)由(1)知,抛物线的解析式为![]() ,则B(0,﹣2).
,则B(0,﹣2).
设直线BC的解析式为:y=kx+d(k≠0).
把B(0,﹣2)、C(3,﹣1)代入,得![]() .
.
解得 .
.
故直线BC的解析式为 ![]() .
.
∴E(t,![]() t﹣2)
t﹣2)
∴S△POE=![]() t(
t(![]() t-2)=
t-2)=![]() (t-3)2-
(t-3)2-![]() .
.
∴△POE面积的最大值是![]() ;
;
(3)存在这样的t值.
理由:E(t,![]() ),F(t,
),F(t,![]() ).
).
若以点C,D,E,F为顶点的四边形是平行四边形,则EF=CD=1,
即﹣(![]() )﹣(2﹣
)﹣(2﹣![]() t)=1.
t)=1.
整理得:7t2﹣21t+12=0.
∵△=(﹣21)2﹣4×7×12>0,
∴方程7t2﹣21t+12=0有解.
∴存在这样的t值:以点C,D,E,F为顶点的四边形是平行四边形.


科目:初中数学 来源: 题型:
【题目】王爷爷上午8:00从家出发,外出散步,到老年阅览室看了一会儿报纸,继续以相同的速度散步一段时间,然后回家.如图描述了王爷爷在散步过程中离家的路程s(米)与所用时间t(分)之间的函数关系,则下列信息错误的是( )

A. 王爷爷看报纸用了20分钟
B. 王爷爷一共走了1600米
C. 王爷爷回家的速度是80米/分
D. 上午8:32王爷爷在离家800米处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
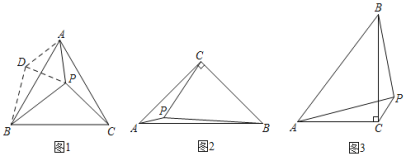
小明遇到这样一个问题:如图1,点P在等边三角形ABC内,且∠APC=150°,PA=3,PC=4,求PB的长.
小明发现,以AP为边作等边三角形APD,连接BD,得到△ABD;由等边三角形的性质,可证△ACP≌△ABD,得PC=BD;由已知∠APC=150°,可知∠PDB的大小,进而可求得PB的长.
(1)请回答:在图1中,∠PDB= °,PB= .
(问题解决)
(2)参考小明思考问题的方法,解决下面问题:
如图2,△ABC中,∠ACB=90°,AC=BC,点P在△ABC内,且PA=1,PB=![]() ,PC=
,PC=![]() ,求AB的长.
,求AB的长.
(灵活运用)
(3)如图3,在Rt△ABC中,∠ACB=90°,∠BAC=α,且tanα=![]() ,点P在△ABC外,且PB=3,PC=1,直接写出PA长的最大值.
,点P在△ABC外,且PB=3,PC=1,直接写出PA长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
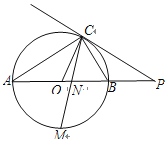
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
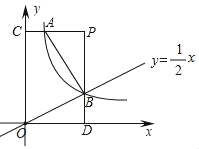
【题目】如图,双曲线y=![]() (x>0)的图象经过点A(
(x>0)的图象经过点A(![]() ,4),直线y=
,4),直线y=![]() x与双曲线交于B点,过A,B分别作y轴、x轴的垂线,两线交于P点,垂足分别为C,D.
x与双曲线交于B点,过A,B分别作y轴、x轴的垂线,两线交于P点,垂足分别为C,D.
(1)求双曲线的解析式;
(2)求证:△ABP∽△BOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的盒子,甲盒中装有编号为1,2,3三个球,乙盒中装有编号为4,5,6三个球,每个盒子中的球除编号外其它完全相同,将盒子中的球摇均后,从每个盒子中随机各取一个球.
(1)从甲盒中取出的球号数是3的概率是 ;
(2)请用列表法或画树状图法,求从两个盒子中取出的球号数都是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
下列说法不正确的是( )

A. 当n很大时,估计指针落子在”铅笔“区域的概率大约是0.70
B. 假如你去转动转盘一次,获得“铅笔”概率大约是0.70
C. 如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次
D. 转动转盘20次,一定有6次获得“文具盒”
查看答案和解析>>
科目:初中数学 来源: 题型:
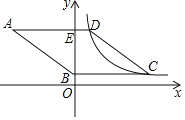
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1=﹣x2时,都有y1=y2,称该函数为偶函数,根据以上定义,可以判断下面所给的函数中,是偶函数的有_____(填上所有正确答案的序号)
①y=2x;②y=﹣x+1;③y=x2;④y=﹣![]() ;⑤y=x2+3;⑥y=x2+2x+1.
;⑤y=x2+3;⑥y=x2+2x+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com