
【题目】如图,∠AOB内有一点P

(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D
(2)写出图中互补的角
(3)写出图中相等的角
(4)试说明图某一对相等.
【答案】(1)见解析;(2)∠O与∠ODP、∠OCP互补;∠CPD与∠ODP、∠OCP互补;∠BDP与∠ODP互补;∠PCA与∠OCP互补;(3)∠O=∠ACP=∠PDB=CPD,∠OCP=∠ODP;(4)∠O=∠ACP,见解析
【解析】
(1)根据平行线的画法作出PC∥OB;根据平行线的画法作出PD∥OA;
(2)根据两直线平行,同旁内角互补;邻补角互补,以及等量代换找出互补的角即可;
(3)根据两直线平行,同位角相等;对顶角相等,以及等量代换找出相等的角即可;
(4)根据平行线的性质即可证明∠O=∠ACP.
(1)如图所示;

(2)∵PC∥OB,
∴∠O与∠OCP互补,∠CPD与∠ODP互补;
∵PD∥OA
∴∠O与∠ODP互补、∠CPD与∠OCP互补;
∵B,D,O在同一直线上,
∴∠BDP与∠ODP互补;
∵A,C,O在同一直线上,
∴∠PCA与∠OCP互补
故图中互补的角有:∠O与∠ODP、∠OCP互补;∠CPD与∠ODP、∠OCP互补;∠BDP与∠ODP互补;∠PCA与∠OCP互补;
(3)∵PC∥OB,
∴∠O=∠ACP,∠CPD=∠PDB,
∵PD∥OA
∴∠O=∠PDB,∠ACP=CPD,
∴∠O=∠CPD,∠OCP=∠ODP,∠ACP=∠PDB,
故图中相等的角有:∠O=∠ACP=∠PDB=CPD,∠OCP=∠ODP;
(4)∵PC∥OB,
∴∠O=∠ACP.


科目:初中数学 来源: 题型:
【题目】高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车站,然后再转车出租车取游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.
请结合图象解决下面问题:

(1)高铁的平均速度是每小时多少千米?
(2)当颖颖达到杭州火车东站时,乐乐距离游乐园还有多少千米?
(3)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下叙述正确的有( )
①对顶角相等;②同位角相等;③两直角相等;④邻补角相等;⑤多边形的外角和都相等;⑥三角形的中线把原三角形分成面积相等的两个三角形
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )

A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
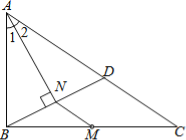
(1)求证:BN=DN;
(2)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在![]() ,
,![]() 两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是
两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是![]() 元,且随身听的单价比书包的单价的
元,且随身听的单价比书包的单价的![]() 倍少
倍少![]() 元.
元.
(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市![]() 所有商品打八五折销售,超市
所有商品打八五折销售,超市![]() 全场购物每满
全场购物每满![]() 元返购物券
元返购物券![]() 元销售(不足
元销售(不足![]() 元不返券,购物券全场通用),但他只带了
元不返券,购物券全场通用),但他只带了![]() 元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
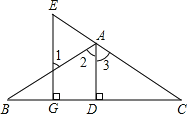
【题目】如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:AD平分∠ABC.下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC(已知)
∴∠ADC=∠EGC=90°( )
∴EG∥AD( )
∴∠E=________( )、
∠1=__________( )
又∵∠E=∠1(已知)
∴∠2=∠3( )
∴AD平分∠BAC ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com