
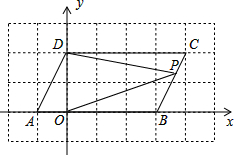
 在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b-2|+$\sqrt{2a-b+5}$=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.
在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b-2|+$\sqrt{2a-b+5}$=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.分析 (1)根据非负数的性质求出a、b的值得出点A、B的坐标,再由平移可得点C、D的坐标,即可知答案;
(2)分点E在x轴和y轴上两种情况,设出坐标,根据S△BCE=S四边形ABDC列出方程求解可得;
(3)作PE∥AB,则PE∥CD,可得∠DCP=∠CPE、∠BOP=∠OPE,继而知∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,即可得答案.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{a+b=2}\\{2a-b=-5}\end{array}\right.$,
解得:a=-1,b=3.
所以A(-1,0),B(3,0),C(0,2),D(4,2),
如图,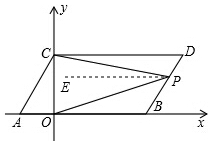
(2)∵AB=3-(-1)=3+1=4,
∴S四边形ABDC=4×2=8;
∵S△BCE=S四边形ABDC,
当E在y轴上时,设E(0,y),
则$\frac{1}{2}$•|y-2|•3=8,
解得:y=-$\frac{10}{3}$或y=$\frac{22}{3}$,
∴$E(0,\frac{22}{3})(0,-\frac{10}{3})$;
当E在x轴上时,设E(x,0),
则$\frac{1}{2}$•|x-3|•2=8,
解得:x=11或x=-5,
∴E(-5,0),(11,0);
(3)由平移的性质可得AB∥CD,
如图,过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
即∠DCP+∠BOP=∠CPO,
所以比值为1.
点评 本题主要考查非负数的性质、一元一次方程的应用、平行四边形的性质及平行线的判定与性质,根据非负数性质求得四点的坐标是解题的根本,熟练掌握平行线的判定与性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
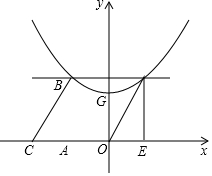 如图,Rt△ABC中,∠A=90°,∠C=60°,AC在x轴上,点C坐标为(-2,0)抛物线y=ax2+$\frac{2}{3}\sqrt{3}$经过点B,其中△EDO是由△ABC沿x轴向右平移得到,且点D在该抛物线上.已知点G为抛物线的顶点.
如图,Rt△ABC中,∠A=90°,∠C=60°,AC在x轴上,点C坐标为(-2,0)抛物线y=ax2+$\frac{2}{3}\sqrt{3}$经过点B,其中△EDO是由△ABC沿x轴向右平移得到,且点D在该抛物线上.已知点G为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
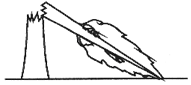 如图,一场大风后,一棵大树在高于地面1米处折断,大树顶部落在距离大树底部3米处的地面上,那么树高是( )
如图,一场大风后,一棵大树在高于地面1米处折断,大树顶部落在距离大树底部3米处的地面上,那么树高是( )| A. | 4m | B. | $\sqrt{10}$m | C. | ($\sqrt{10}$+1)m | D. | ($\sqrt{10}$+3)m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
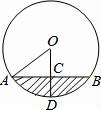 如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,求(1)水的最大深度CD(2)若角AOD为50度,求阴影部分的面积.
如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,求(1)水的最大深度CD(2)若角AOD为50度,求阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
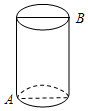 如图,有一圆柱,其高为8cm,它的底面半径2cm,在下底面点A处有一只蚂蚁,它想得到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程为10cm cm(注:π取3).
如图,有一圆柱,其高为8cm,它的底面半径2cm,在下底面点A处有一只蚂蚁,它想得到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程为10cm cm(注:π取3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com