
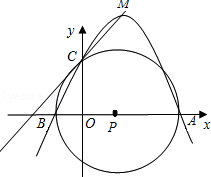
 (2)
(2) (3)MC与⊙P的位置关系是相切
(3)MC与⊙P的位置关系是相切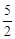 。∴OP=
。∴OP= 。
。 。∴C(0,2)。
。∴C(0,2)。 ,
, ,∴
,∴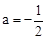 。
。 。
。 ,
, ,∴M
,∴M 。
。 代入得:
代入得: ,解得
,解得 。
。 。
。
 ,∴
,∴ ,OD=
,OD= 。∴D(
。∴D( ,0)。
,0)。 ,
, ,
, ,
, ,把C(0,2)代入求出a即可。
,把C(0,2)代入求出a即可。 代入得到方程组,求出方程组的解即可。
代入得到方程组,求出方程组的解即可。

 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
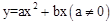 。
。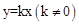 上,请用含k的代数式表示b;
上,请用含k的代数式表示b;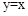 上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 元.
元.
 的值;
的值; (万元)时,产品的年销售量将是原来年销售量的
(万元)时,产品的年销售量将是原来年销售量的 倍,且
倍,且 与
与 之间的关系满足
之间的关系满足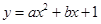 .请根据图象提供的信息,求出
.请根据图象提供的信息,求出 与
与 之间的函数关系式;
之间的函数关系式; (万元)之间的函数关系式,并请回答广告费
(万元)之间的函数关系式,并请回答广告费 (万元)在什么范围内,公司获得的年利润S(万元)随广告费的增大而增多?(注:年利润S=年销售总额-成本费-广告费)
(万元)在什么范围内,公司获得的年利润S(万元)随广告费的增大而增多?(注:年利润S=年销售总额-成本费-广告费)查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=3x2+2 | B.y=3(x﹣1)2 |
| C.y=3(x﹣1)2+2 | D.y=2x2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
温度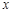 /℃ /℃ | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 /mm /mm | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
 是温度
是温度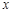 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.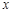 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com