
【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .
【答案】50°.
【解析】
利用全等三角形的判定以及垂直平分线的性质得出∠OBC=40°,以及∠OBC=∠OCB=40°,再利用翻折变换的性质得出EO=EC,∠CEF=∠FEO,进而求出即可;
连接BO,

∵AB=AC,AO是∠BAC的平分线,
∴AO是BC的中垂线.
∴BO=CO.
∵∠BAC=50°,∠BAC的平分线与AB的中垂线交于点O,
∴∠OAB=∠OAC=25°.
∵等腰△ABC中, AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=65°.
∴∠OBC=65°-25°=40°.
∴∠OBC=∠OCB=40°.
∵点C沿EF折叠后与点O重合,
∴EO=EC,∠CEF=∠FEO.
∴在△OEC中,
∠CEF=∠FEO=(180°-2×40°)÷2=50°.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,给定∠AOB=60°,及OB边上一点C,如图所示.到射线OA,OB距离相等的所有点组成图形G,线段OC的垂直平分线交图形G于点D,连接CD.
(1)依题意补全图形;直接写出∠DCO的度数;
(2)过点D作OD的垂线,交OA于点E,OB于点F.求证:CF=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,已知
,已知![]() 中,
中,![]() ,
,![]() ,
,![]() 的顶点
的顶点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,当点
上,当点![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在
随之在![]() 上运动,
上运动,![]() 的形状始终保持不变,在运动的过程中,点
的形状始终保持不变,在运动的过程中,点![]() 到点
到点![]() 的最小距离为( )
的最小距离为( )

A. 5 B. 7 C. 12 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )

A. ![]() 是等边三角形
是等边三角形
B. 连接![]() ,则
,则![]() 分别平分
分别平分![]() 和
和![]()
C. 整个图形是轴对称图形,但不是中心对称图形
D. 四边形![]() 与四边形
与四边形![]() 的面积相等
的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )
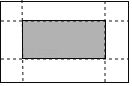
A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市计划建造一座如图设计的塔形建筑物作为市标,最底层的圆柱形的底面半径为![]() ,高为
,高为![]() 米,再上去的圆柱形底面半径以
米,再上去的圆柱形底面半径以![]() 的比例缩小,而楼层的高度也以同样的比例缩小,那么要使得建筑物的表面积不超过
的比例缩小,而楼层的高度也以同样的比例缩小,那么要使得建筑物的表面积不超过![]() 平方米(表面积不包括最底层的底面积),楼层最高为________层.
平方米(表面积不包括最底层的底面积),楼层最高为________层.![]() 取
取![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com