
【题目】某公司为了更好得节约能源,决定购买一批节省能源的10台新机器。现有甲、乙两种型号的设备,其中每台的价格、工作量如下表。经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台甲型设备比购买3台乙型设备少6万元.
甲型 | 乙型 | |
价格(万元/台) |
|
|
产量(吨/月) | 240 | 180 |
(1)求a, b的值;
(2)经预算:该公司购买的节能设备的资金不超过110万元,请列式解答有几种购买方案可供选择;
(3)在(2)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
【答案】(1)a, b的值分别是12,10
(2)6
(3)最省钱的购买方案为,应选购A型设备4台,B型设备6台
【解析】
试题分析:解:(1)由题意可知:![]()
![]() -----------------------------------------------------3分
-----------------------------------------------------3分
答:a, b的值分别是12,10.
(2)设购买A型设备x台,B型设备(10-x)台,则:
12x+10(10-x)≤110------------------------------4分
∴x≤5,∵x取非负整数∴x=0,1,2,3,4,5,
![]() 有6种购买方案-----------------------6分
有6种购买方案-----------------------6分
(3)由题意:240x+180(10-x)≥2040-------------------------------7分
∴x≥4∴x为4或5.--------------------------------------8分
当x=4时,购买资金为:12×4+10×6=108(万元)
当x=5时,购买资金为:12×5+10×5=110(万元)
![]() 最省钱的购买方案为,应选购A型设备4台,B型设备6台-----------9分
最省钱的购买方案为,应选购A型设备4台,B型设备6台-----------9分


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解答问题:
材料1 从3张不同的卡片中选取2张排成一列,有6种不同的排法,抽象成数学问题就是从3个不同元素中选取2个元素的排列,排列数记为A32=3×2=6.
一般地,从n个不同元素中选取m个元素的排列数记作Anm ,
Anm=n(n-1)(n-2)…(n-m+1)(m≤n).
例:从5个不同元素中选3个元素排成一列的排列数为:A53=5×4×3=60.
材料2 从3张不同的卡片中选取2张,有3种不同的选法,抽象成数学问题就是从3个元素中选取2个元素的组合,组合数记为C32=![]() =3.
=3.
一般地,从n个不同元素中选取m个元素的组合数记作Cnm ,
Cnm= ![]() (m≤n).
(m≤n).
例:从6个不同元素中选3个元素的组合数为:
C63=![]() =20.
=20.
问:(1)从7个人中选取4人排成一排,有多少种不同的排法?
(2)从某个学习小组8人中选取3人参加活动,有多少种不同的选法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一组邻边相等,并且有一个角是直角的平行四边形是正方形,因此正方形是四边相等,四角相等的四边形.
初二数学兴趣小组开展了一次课外活动,过程如下:如图,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.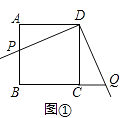
(1)求证:DP=DQ
(2)如图②,小聪在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;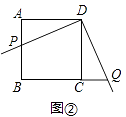
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小聪算出△DEP的面积.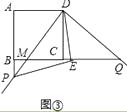
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:
梯形的中位线平行于两底,并且等于两底和的一半.
如图(1):在梯形ABCD中:AD∥BC
∵E、F是AB、CD的中点
∴EF∥AD∥BC
EF=![]() (AD+BC)
(AD+BC)
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
如图(2):在△ABC中:
∵E是AB的中点,EF∥BC
∴F是AC的中点
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°
请你运用所学知识,结合上述材料,解答下列问题.
(1)求证:EF=AC;
(2)若OD=![]() ,OC=5,求MN的长.
,OC=5,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】原子很小,1010个氧原子首位连接排成一行的长度为1m,则每一个氧原子的直径为( )
A.10﹣7m
B.10﹣8m
C.10﹣9m
D.10﹣10m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com