练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，菱形ABCD中，AB=5，∠BCD=120°，则对角线AC的长是(　　)

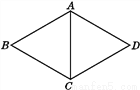
    A. 20 B. 15 C. 10 D. 5

    B 【解析】试题解析： 是菱形, 是等边三角形. 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：单选题

    下图中射线OA与OB表示同一条射线的是(　　)

    A. （A） B. （B） C. （C） D. （D）

    B 【解析】试题解析：A、方向相反，故A不是同一条射线； B、端点相同，方向相同，故C是同一条射线； C、方向不同，故D不是同一条射线； D、方向相反，故B不是同一条射线； 故选B．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    有一个二次函数的图象，三位同学分别说了它的一些特点：

    甲：与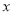轴只有一个交点；

    乙：对称轴是直线；

    丙：与y轴的交点到原点的距离为3．

    满足上述全部特点的二次函数的解析式为______________________．

    或 【解析】试题解析: ∵二次函数的对称轴为直线x=3， ∴k=3， ∴二次函数的解析式为 ∵与y轴的交点到原点的距离为3， ∴与y轴交于点(0,3)或(0,?3)， 把(0,3)代入得， 把(0,?3)代入得， ∴解析式为： 或. 故答案为： 或.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：解答题

    已知：如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E，∠1=∠2．

    （1）若CE=1，求BC的长；

    （2）求证：AM=DF+ME．

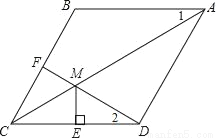
    (1)2;(2)见解析. 【解析】试题分析：（1）根据菱形的对边平行可得AB∥CD，再根据两直线平行，内错角相等可得∠1=∠ACD，所以∠ACD=∠2，根据等角对等边的性质可得CM=DM，再根据等腰三角形三线合一的性质可得CE=DE，然后求出CD的长度，即为菱形的边长BC的长度； （2）先利用“边角边”证明△CEM和△CFM全等，根据全等三角形对应边相等可得ME=MF，延长AB交DF于点G...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：填空题

    如图，在矩形ABCD中，点E、F分别在AB、DC上，BF∥DE，若AD=12cm，AB=7cm，且AE：EB=5：2，则阴影部分的面积为_______

    24cm2． 【解析】试题分析：因为AD=12cm，AB=7cm，且AE：BE=5：2，则AE=5，BE=2， 则阴影部分的面积=12×7﹣12×5=24cm2． 故答案是24cm2．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：单选题

    正多边形的一个内角是120°，则这个正多边形的边数为(　　)

    A. 4 B. 8 C. 6 D. 12

    C 【解析】根据正多边的内角求出外角为180°-120°=60°，然后根据多边形的外角和为360°，可求其边数为360÷60°=6. 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：解答题

    已知：b是最大的负整数，且a，b，c满足|a+b|+（4－c）2016 =0，试回答问题：

    （1）请直接写出a，b，c的值；

    （2）若a，b，c所对应的点分别为A，B，C，点P为一动点，其对应的数为x，点P在0到1之间运动时（即0≤x≤1），请化简式子：|x+1|－|1-x|+2|x－4|；

    （3）在（1）、（2）的条件下，点A，B，C开始在数轴上运动，若点A以每秒2个单位长度的速度向左运动，同时，点B和C分别以每秒3个单位长度和8个单位长度的速度向右运动，假设t秒后，若点B与点C之间的距离表示为BC，点A与B之间的距离表示为AB．请问：AB-BC的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．

    （1） a=-1，b=1，c=4；（2）8；（3） AB-BC的值是否随着时间t的变化而改变. 【解析】分析：（1）根据b是最大的负整数，即可得出b的值，再根据绝对值及偶次方的非负性即可得出a、c的值；（2）分析当0≤x≤1时，x+1、1-x、x-4的正负，去掉绝对值符号即可得出结论；（3）找出运动时间为t时，点A、B、C对应的数，再根据两点间的距离公式找出AB、BC的长度，二者做差后即可得...

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：解答题

    如图所示，沿海城市B的正南方向A处有一台风中心，沿AC的方向以30km/h的速度移动，已知AC所在的方向与正北成30°的夹角，B市距台风中心最短的距离BD为120km，求台风中心从A处到达D处需要多少小时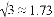？（，结果精确到0.1）

    6.9小时 【解析】试题分析：根据30°角所对的边等于斜边的一半得出AB的长度，然后根据直角三角形的勾股定理求出AD的长度，然后根据时间的计算法则求出答案． 试题解析：【解析】 在Rt△ADB中，∠ADB=90°， ∵∠BAD=30°，BD=120km， ∴AB=2BD=240km， 根据勾股定理得：AD==120km， ∵≈1.73， ∴从A到D处需要=4≈6.9小时．...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：单选题

    如图，已知双曲线y=（k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣6，4），则△AOC的面积为（　　）

    A. 12 B. 9 C. 6 D. 4

    B 【解析】试题分析：△AOC的面积=△AOB的面积-△BOC的面积，由点A的坐标为（-6，4），根据三角形的面积公式，可知△AOB的面积=12，由反比例函数的比例系数k的几何意义，可知△BOC的面积=|k|．只需根据OA的中点D的坐标，求出k值即可． 试题解析：∵OA的中点是D，点A的坐标为（-6，4）， ∴D（-3，2）， ∵双曲线y=经过点D， ∴k=-3×2=...

    查看答案和解析>>

    同步练习册答案