
【题目】如图,是一系列用同样规格的黑白两色正方形瓷砖铺设长方形地面.请观察并解答下列问题:
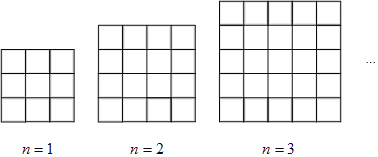
(1)在第n个图形中,共有多少块黑瓷砖(用含n的代数式表示);
(2)设铺设地面所用瓷砖的总块数为y,用(1)中的n表示y;
(3)当n=12时,求y的值;
(4)若黑瓷砖每块3元,白瓷砖每块2元,在问题(3)中,试求共需花多少元购买瓷砖.
【答案】(1)在第n个图形中,共有黑瓷砖的块数为(4n+4)块;(2)y=(n+2)2;(3)196;(4)共需花444元购买瓷砖
【解析】
(1)根据图形的变化即可求出在第n个图形中,共有多少块黑瓷砖;
(2)设铺设地面所用瓷砖的总块数为y,用(1)中的n即可表示y;
(3)当n=12时,代入值即可求y的值;
(4)根据黑瓷砖每块3元,白瓷砖每块2元,在问题(3)中,即可求共需花多少元购买瓷砖.
解:(1)观察图形的变化可知,
在第1个图形中,共有黑瓷砖的块数为4×1+4=8;
在第2个图形中,共有黑瓷砖的块数为4×2+4=12;
在第3个图形中,共有黑瓷砖的块数为4×3+4=16;
…
在第n个图形中,共有黑瓷砖的块数为(4n+4)块;
(2)设铺设地面所用瓷砖的总块数为y,
根据图形的变化可知:y=(n+2)2;
(3)当n=12时,y=(12+2)2=196;
(4)当n=12时,
黑瓷砖有:4n+4=52(块),
白瓷砖有:196﹣52=144(块),
所以3×52+2×144=444(元).
答:共需花444元购买瓷砖.


科目:初中数学 来源: 题型:
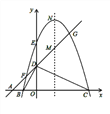
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.
(1)求经过B、E、C三点的抛物线的解析式;
(2)若点P为线段FG上一个动点(与F、G不重合),当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,请求出此时点P的坐标;
(3)若点P为直线FG上一个动点,Q为抛物线上任一点,抛物线的顶点为N,探究以P、Q、M、N为顶点的四边形能否成为平行四边形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
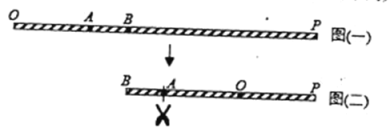
【题目】如图(一),![]() 为一条拉直的细线,
为一条拉直的细线,![]() 两点在
两点在![]() 上,且
上,且![]() . 若先固定
. 若先固定![]() 点,将
点,将![]() 折向
折向![]() ,使得
,使得![]() 重迭在BP上,如图(二);再从图(二)的
重迭在BP上,如图(二);再从图(二)的![]() 点及与
点及与![]() 点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为( )
点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
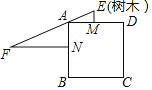
【题目】《九章算术》记载“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方有几何?”意思是:如图,点M、点N分别是正方形ABCD的边AD、AB的中点,ME⊥AD,NF⊥AB,EF过点A,且ME=30步,NF=750步,则正方形的边长为( )
A. 150步B. 200步C. 250步D. 300步
查看答案和解析>>
科目:初中数学 来源: 题型:
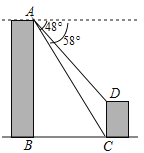
【题目】如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求乙建筑物的高度CD.(结果取整数,参考数据:tan58°≈1.60,tan48°≈1.11).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() 将一直角三角板的直角顶点放在点
将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方.
的下方.
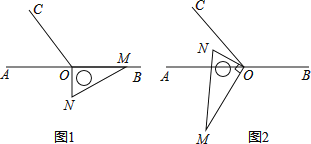
(1)将图1中的三角板绕点![]() 按每秒
按每秒![]() 的速度沿顺时针方向旋转,使
的速度沿顺时针方向旋转,使![]() 落在
落在![]() 上.在旋转的过程中,假如第
上.在旋转的过程中,假如第![]() 秒时,
秒时,![]() 、
、![]() 、
、![]() 三条射线构成的角中有两个角相等,求此时
三条射线构成的角中有两个角相等,求此时![]() 的值为多少?
的值为多少?
(2)将图1中的三角板绕点![]() 顺时针旋转(如图2),使
顺时针旋转(如图2),使![]() 在
在![]() 的内部,请探究:
的内部,请探究:![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连接CD.若AB=4cm.则△BCD的面积为( )

A. 4![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:其中正确的个数是()
(1)有一个角为60°的等腰三角形是等边三角形;
(2)三角之比为3:4:5的三角形为直角三角形;
(3)等腰三角形的两条边长为2,4,则等腰三角形的周长为10;
(4)一边上的中线等于这边长的一半的三角形是等边三角形;
A.2个B.3个C.4个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com