
分析 分为两种情况①当AC=5,BC=12时,由勾股定理求出AB,根据直角三角形斜边上中线得出CD=$\frac{1}{2}$AB,求出即可;
②当AC=5,AB=12时,根据直角三角形斜边上中线得出CD=$\frac{1}{2}$AB,求出即可.
解答 解: 分为两种情况:①当AC=5,BC=12时,
分为两种情况:①当AC=5,BC=12时,
由勾股定理得:AB=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∵CD是斜边AB上的中线,
∴CD=$\frac{1}{2}$AB=6.5;
②当AC=5,AB=12时,
∵CD是斜边AB上的中线,
∴CD=$\frac{1}{2}$AB=6;
即CD=6.5或6,
故答案为:6.5或6.
点评 本题考查了勾股定理和直角三角形斜边上中线性质,注意:①直角三角形斜边上中线等于斜边的一半,②要进行分类讨论.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
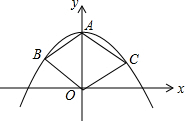 如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的图象过菱形ABOC的三个顶点A、B、C,∠BAC=120°,则ac的值是-$\frac{2}{3}$.
如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的图象过菱形ABOC的三个顶点A、B、C,∠BAC=120°,则ac的值是-$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
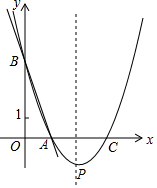 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=(x-h)2+k经过点A、B,其顶点为P.在抛物线的对称轴上是否存在一点Q,连接QA、QB,并将△ABQ沿AB翻折,得到菱形AQBQ′?若存在,请求出点Q的坐标;若不存在,说明理由.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=(x-h)2+k经过点A、B,其顶点为P.在抛物线的对称轴上是否存在一点Q,连接QA、QB,并将△ABQ沿AB翻折,得到菱形AQBQ′?若存在,请求出点Q的坐标;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com