
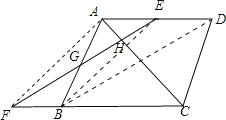
【题目】如图,菱形ABCD中,E是AD的中点,EF⊥AC交CB的延长线于点F.
(1)DE和BF相等吗?请说明理由.
(2)连接AF、BE,四边形AFBE是平行四边形吗?说明理由.

【答案】(1)、相等,理由见解析;(2)、是,理由见解析.
【解析】试题分析:(1)、连接BD,AF,BE,根据菱形的性质得出AC⊥BD,结合EF⊥AC得出EF∥BD,结合ED∥FB得出四边形EDBF是平行四边形,从而得出结论;(2)、根据E为AD的中点得出AE=ED,则AE=BF,结合AE∥BF得出四边形AEBF为平行四边形,从而说明结论.
试题解析:(1)、连接BD,AF,BE, 在菱形ABCD中,AC⊥BD ∵EF⊥AC,
∴EF∥BD,又ED∥FB, ∴四边形EDBF是平行四边形,DE=BF,
(2)、∵E为AD的中点, ∴AE=ED,∴AE=BF, 又AE∥BF, ∴四边形AEBF为平行四边形,
即AB与EF互相平分.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
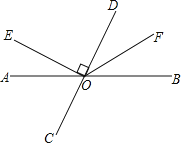
【题目】如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD.
(1)图中除直角外,请写出一对相等的角吗: (写出符合的一对即可)
(2)如果∠AOE=26°,求∠BOD和∠COF的度数.(所求的角均小于平角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象a过点M(﹣1,﹣4.5),N(1,﹣1.5)
(1)求此函数解析式,并画出图象;
(2)求出此函数图象与x轴、y轴的交点A、B的坐标;
(3)若直线a与b相交于点P(4,m),a、b与x轴围成的△PAC的面积为6,求出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( ) ①﹣(﹣3)的相反数是﹣3
②近似数1.900×105精确到百位
③代数式|x+2|﹣3的最小值是0
④两个六次多项式的和一定是六次多项式.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
操作发现:
(1)已知,△ABC,如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图 , 并猜想BE与CD的数量关系是 . (要求:尺规作图,不写作法但保留作图痕迹)
类比探究: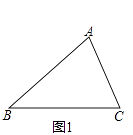
(2)如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么关系?说明理由.
灵活运用: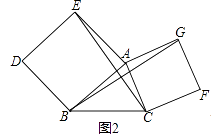
(3)如图3,已知△ABC中,∠ABC=45°,AB=2 ![]() ,BC=3,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.
,BC=3,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.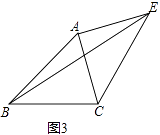
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com