
����Ŀ��ijѧУҪ��չУ�����ڻ��Ϊ�˺������Ž�Ŀ����ѧ����ϲ���ĸ������赸��СƷ�����������Ŀ������һ������������飨ÿ��ѧ������ѡ����ֻ��ѡ��һ�ࣩ���������������Ƴ�����������������ͳ��ͼ.
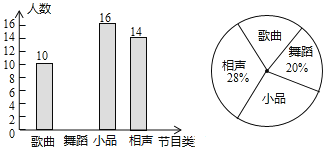
�����ͼ����Ϣ���ش��������⣺
��1�����ι�������_________��ѧ��.
��2��������ͳ��ͼ�У����������������ε�Բ�Ľǵ���_________��.
��3����ȫ����ͳ��ͼ������עƵ����.
��4����������ͳ�Ʒ��������Ƹ�У2000��ѧ������ϲ��СƷ������Լ�ж�������
���𰸡���1��50����2��72����3��ͼ�ԣ���4��2000��ѧ������ϲ��СƷ������Լ��640����
��������
��1��������ͳ��ͼ�пɵ�ϲ����������������Ϊ14�ˣ�ռ����������28%�����������������
��2����360����������С���������ռ�ıȼ��ɣ�
��3�������ϲ�����赸���������ٲ�ȫ����ͳ��ͼ��
��4�������������壬��������2000���������С�СƷ����ռ�ıȣ�
��1��14��28%=50��������
�ʴ�Ϊ��50��
��2��360��![]() 72�㣮
72�㣮
�ʴ�Ϊ��72��
��3��50��10��16��14=10����������ȫ����ͳ��ͼ��ͼ��ʾ��
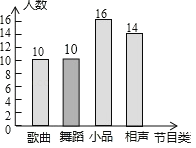
��4��2000![]() 640��������
640��������
�𣺸�У2000��ѧ������ϲ��СƷ������Լ��640����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ͷ���½���һ�̳�����������30�䣬���Ʋ⣬��ÿ��������Ϊ10��Ԫʱ����ȫ���������ÿ��������ÿ����5000Ԫ�����������1�䣬�ù�˾ҪΪ���������ÿ��ÿ�꽻���ַ���1��Ԫ��δ���������ÿ��ÿ�꽻���ַ���5000Ԫ��
��1����ÿ�����̵������Ϊ12��Ԫʱ����������ټ䣿
��2����ÿ�����̵������Ϊ������Ԫʱ���ù�˾��������Ϊ285��Ԫ��������=��𩁸��ַ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ(1)��ABΪ��ԲO��ֱ����DΪBA���ӳ�����һ�㣬DCΪ��ԲO�����ߣ��е�ΪC��
��1����֤����ACD=��B��
��2����ͼ(2)����BDC��ƽ���߷ֱ�AC��BC�ڵ�E��F�����CEF�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABCD�У�BC=2AB��M��AD���е㣬CE��AB������ΪE����֤����DME=3��AEM.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
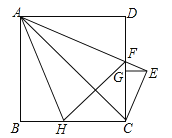
����Ŀ����ͼ���߳�Ϊ2��������ABCD�У�AEƽ�֡�DAC��AE��CD�ڵ�F��CE��AE������Ϊ��E��EG��CD������Ϊ��G����H�ڱ�BC�ϣ�BH=DF������AH��FH��FH��AC���ڵ�M�����½��ۣ�
��FH=2BH����AC��FH����S��ACF=1����CE=![]() AF����
AF����![]() =FGDG��������ȷ���۵ĸ���Ϊ��������
=FGDG��������ȷ���۵ĸ���Ϊ��������
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ABCD��,E��AD���е�,����ABE��ֱ��BE�۵���õ���GBE,�ӳ�BG��CD�ڵ�F. ��AB=6,BC=![]() ,��FD�ij�Ϊ( )
,��FD�ij�Ϊ( )
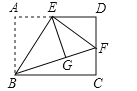
A. 2B. 4C. 6D. 23
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���C�İ뾶Ϊr��P����Բ��C���غϵĵ㣬��P������C�ķ��Ƶ�Ķ������£���������CP�ϴ���һ��P�䣬����CP+CP��=2r�����P��Ϊ��P������C�ķ��Ƶ㣬��ͼΪ��P���������C�ķ��Ƶ�P���ʾ��ͼ��
�ر�أ�����P����Բ��C�غ�ʱ���涨CP��=0��
��1������O�İ뾶Ϊ1ʱ��
���ֱ��жϵ�M��2��1����N��![]() ��0����T��1��
��0����T��1�� ![]() ��������O�ķ��Ƶ��Ƿ���ڣ������ڣ��������ꣻ
��������O�ķ��Ƶ��Ƿ���ڣ������ڣ��������ꣻ
����P��ֱ��y=��x+2�ϣ�����P������O�ķ��Ƶ�P����ڣ��ҵ�P�䲻��x���ϣ����P�ĺ������ȡֵ��Χ��
��2����C��Բ����x���ϣ��뾶Ϊ1��ֱ��y=��![]() x+2
x+2![]() ��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P������C�ķ��Ƶ�P������C���ڲ�����Բ��C�ĺ������ȡֵ��Χ��
��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P������C�ķ��Ƶ�P������C���ڲ�����Բ��C�ĺ������ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ���ı���ABCD�У�GΪBC�е㣬��E��AD���ϣ��ҡ�1=��2��
(1)��֤��E��AD�е㣻
(2)��FΪCD�ӳ�����һ�㣬����BF���������3=��2����֤��CD=BF+DF��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com