
【题目】如图,在ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.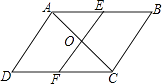
(1)求证:AE=CF;
(2)当EF⊥AC时,连接AF,CE,试判断四边形AFCE是怎样的四边形?并证明你的结论.
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠EAO=∠FCO,
∵O为AC的中点,
∴OA=OC,
在△AOE和△COF中, 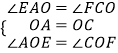 ,
,
∴△AOE≌△COF(ASA),
∴AE=CF;
(2)
解:如图所示:四边形AFCE是菱形;
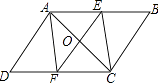
理由如下:
由(1)得:△AOE≌△COF,
∴OE=OF,
∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC,
∴四边形AFCE是菱形.
【解析】(1)由ASA证明△AOE≌△COF,的长对应边相等即可;(2)先由对角线互相平分证出四边形AFCE是平行四边形,再由EF⊥AC,即可证出四边形AFCE是菱形.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


科目:初中数学 来源: 题型:
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段 | 频数 | 频率 |
60≤x<70 | 40 | 0.40 |
70≤x<80 | 35 | b |
80≤x<90 | a | 0.15 |
90≤x<100 | 10 | 0.10 |
频率分布统计表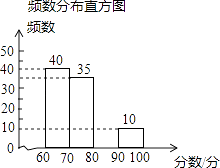
请根据上述信息,解答下列问题:
(1)分别求出a、b的值;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各项目的工作量如图所示: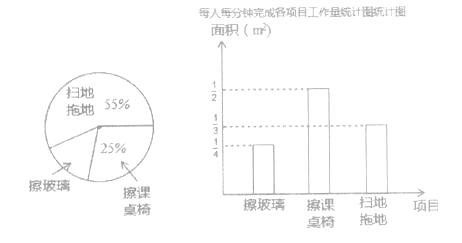
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 , 每人每分钟擦课桌椅
m2;
(2)扫地拖地的面积是m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?(要有详细的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
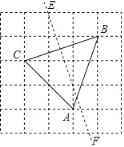
【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点和线段EF的两个端点都在小正方形的格点(顶点)上,小明在观察探究时得到以下四个结论:
①△ABC是等边三角形;②△ABC的周长是![]() ;
;
③△ABC的面积是4;④直线EF是线段BC的垂直平分线.
你认为以上结论中,正确的序号有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于 . 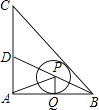
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,
若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值;
(2)若一条直线经过A(2,3),且与y=﹣![]() x+3垂直,求这条直线所对应的一次函数的关系式.
x+3垂直,求这条直线所对应的一次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
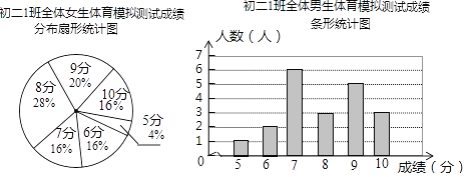
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图描述了某汽车在行驶过程中速度与时间的关系,下列说法中正确的是________.(填序号)

①第3分钟时,汽车的速度是40千米/时;
②第12分钟时,汽车的速度是0千米/时;
③从第3分钟到第6分钟,汽车行驶了120千米;
④从第9分钟到第12分钟,汽车的速度从60千米/时减小到0千米/时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为C.延长AB交CD于点E.连接AC,作∠DAC=∠ACD,作AF⊥ED于点F,交⊙O于点G. 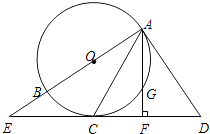
(1)求证:AD是⊙O的切线;
(2)如果⊙O的半径是6cm,EC=8cm,求GF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com