练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．在△ABC中，∠A=30°，三边分别为AB=2，BC=1，AC=$\sqrt{3}$，则∠B=60°．

    分析 先利用勾股定理的逆定理证明△ABC为直角三角形，然后利用互余计算∠B的度数．

    解答 解：∵AB=2，BC=1，AC=$\sqrt{3}$，
    ∴BC2+AC2=1+3=4=AB2，
    ∴△ABC为直角三角形，
    ∴∠B=90°-∠A=90°-30°=60°．
    故答案为60°．

    点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．熟练掌握勾股定理和三角函数的定义是解决此类问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．已知y=$\frac{1}{3}$（x+1）2-2，图象的顶点坐标为（-1，-2），当x＜-1时，函数值随x的增大而减小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．一张正方形纸对折，得到一条折痕，继续对折，对折时每次折痕与上次折痕平行，连续对折3次，得7条折痕；对折4次，得15条折痕；对折n次，得（2n-1）条折痕．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

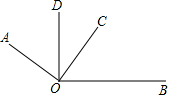    11．如图，∠AOC与∠BOD都是直角．
    （1）∠AOD和∠BOC是什么关系？
    （2）若∠AOB=152°，求∠DOC的度数；
    （4）若∠DOC=x°，求∠AOB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图是由相同边长的正三角形，正方形，正六边形组成的镶嵌图，若外面这一圈阴影部分面积比中间这个正六边形面积大12cm2，则这些正多边形的边长是$\sqrt{2}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知xy：yz：zx=3：2：1，求①x：y：z；②$\frac{x}{yz}$：$\frac{y}{zx}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．（1）计算：m（m+2n）-（m+1）2+2m
    （2）计算：6.290+（-$\frac{1}{2}$）-3-π2016×（-$\frac{1}{π}$）2016．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图①，天平呈平衡状态，其中左侧盘中有一袋玻璃球，右侧盘中也有一袋玻璃球，还有2个各20g的砝码．现将左侧袋中一颗玻璃球移至右侧盘，并拿走右侧盘中的1个砝码，天平仍呈平衡状态，如图②．则移动的玻璃球质量为（　　）
    A．10 gB．15 gC．20 gD．25 g

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

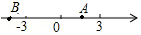    19．点A，B在数轴上的位置如图所示，其对应的数分别是a和b．对于以下结论：
    甲：b-a＜0；乙：a+b＞0；丙：|a|＜|b|；丁：$\frac{b}{a}$＞0
    其中正确的是甲丙．

    查看答案和解析>>

    同步练习册答案