
分析 (1)本题需先表示出第二条边长,即可得出第三条边长.
(2)本题需先求出三边的长,再根据三角形的三边关系列出不等式组,即可求出a的取值范围.
(3)本题需先求出a的值,然后即可得出三角形的三边长.
解答 解:(1)∵第二条边长为2a+2,
∴第三条边长为40-a-(2a+2)=38-3a.
(2)根据题意得:
$\left\{\begin{array}{l}{a+2a+2>38-3a}\\{a+38-3a>2a+2}\\{2a+2+38-3a>a}\end{array}\right.$,
解得:6<a<9.
则a的取值范围是:6<a<9.
(3)在(2)的条件下,注意到a为整数,所以a只能取7或8.
当a=7时,三角形的三边长分别为7,16,17.由72+162≠172知,此时不能构成直角三角形.
当a=8时,三角形的三边长分别为8,18,14.由82+142≠182知,恰此时不能构成直角三角形.
综上所述,不能围成满足条件的小圈是直角三角形形状.
点评 本题主要考查了一元一次不等式组的应用,在解题时要能根据三角形的三边关系,列出不等式组是本题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
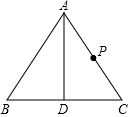 如图,等边三角形ABC,D为BC边的中点,AD=12,P为AC的中点,问在AD是否存在一点Q,使CQ+PQ最小,如果存在,写出作图思路,画出Q的位置,并求出这个最小值;如果不存在,说明理由.
如图,等边三角形ABC,D为BC边的中点,AD=12,P为AC的中点,问在AD是否存在一点Q,使CQ+PQ最小,如果存在,写出作图思路,画出Q的位置,并求出这个最小值;如果不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com