
 如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2.
如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2. 分析 根据垂直平分线的性质可知,AD=DB,由于△ABD的周长比?ABCD的周长少10cm,所以可求出BD=9cm,再根据周长的值求出AB,根据勾股定理求出高DE,即可求出答案.
解答 解:∵AB的垂直平分线EF经过点D,
∴DA=DB,
∵四边形ABCD是平行四边形,
∴DA=CB,
∵△ABD的周长比?ABCD的周长少10cm
∴BD=9cm,
∴ADBC=BD=9cm,
∵?ABCD的周长为42cm,
∴AB=DC=$\frac{1}{2}$×42cm-9cm=12cm,
在△ADB中,AD=BD=9cm,AB=12cm,
∵DE垂直平分AB,
∴∠AED=90°,AE=BE=6cm,由勾股定理得:DE=$\sqrt{{9}^{2}-{6}^{2}}$=3$\sqrt{5}$(cm),
∴S平行四边形ABCD=AB×DE=12cm×3$\sqrt{5}$cm=36$\sqrt{5}$cm2,
故答案为:12,36$\sqrt{5}$.
点评 本题考查了线段垂直平分线和平行四边形的性质,证得AD=BD=BC是解题的关键.


科目:初中数学 来源: 题型:解答题
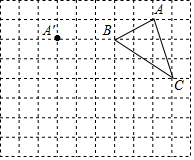 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
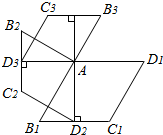 如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°…则AD2=$\frac{\sqrt{3}}{2}$,依此类推这样做的第n个菱形ABnCnDn的边ADn的长是($\frac{\sqrt{3}}{2}$)n-1.
如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°…则AD2=$\frac{\sqrt{3}}{2}$,依此类推这样做的第n个菱形ABnCnDn的边ADn的长是($\frac{\sqrt{3}}{2}$)n-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,若BD与AC的和为23,AB:AD=1:2,△COD的周长为15,求BC的长.
如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,若BD与AC的和为23,AB:AD=1:2,△COD的周长为15,求BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com