
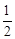 ×(180°-54°)=63°.
×(180°-54°)=63°.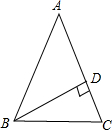
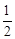 ×(180°-126°),=27°.
×(180°-126°),=27°.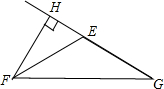


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源:不详 题型:解答题
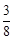 ,求x的值;
,求x的值;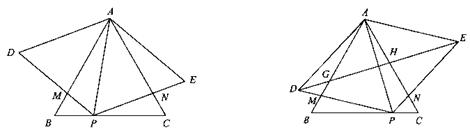
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
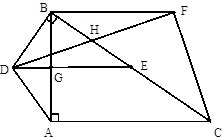
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
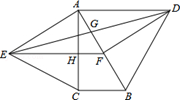
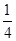 BD;其中正确结论的是( )
BD;其中正确结论的是( )| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
|
如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线  上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( ) 上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com