【题目】已知四边形ABCD是正方形，△ADE是等边三角形，求∠BEC的度数．
【答案】 30°或者150°.
【解析】试题分析：分当等边△ADE在正方形ABCD外部时（如图①）和当等边△ADE在正方形ABCD内部时（如图②）两种情况求解.
试题解析：
(1)当等边三角形ADE在正方形ABCD外部时，如图①所示．
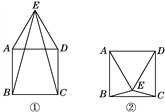
∵AB＝AD＝AE，∠BAE＝90°＋60°＝150°，
∴∠AEB＝(180°－150°)÷2＝15°.
同理，∠DEC＝15°.∴∠BEC＝60°－15°－15°＝30°.
(2)当等边三角形ADE在正方形ABCD内部时，如图②所示．
∵AB＝AD＝AE，∠BAE＝90°－60°＝30°，
∴∠AEB＝(180°－30°)÷2＝75°.
同理，∠DEC＝75°.∴∠BEC＝360°－75°×2－60°＝150°.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】在△ABC中，∠ACB=90°，∠A＜45°，点O为AB中点，一个足够大的三角板的直角顶点与点O重合，一边OE经过点C，另一边OD与AC交于点M．
（1）如图1，当∠A=30°时，求证：MC2=AM2+BC2；
（2）如图2，当∠A≠30°时，（1）中的结论是否成立？如果成立，请说明理由；如果不成立，请写出你认为正确的结论，并说明理由；
（3）将三角形ODE绕点O旋转，若直线OD与直线AC相交于点M，直线OE与直线BC相交于点N，连接MN，则MN2=AM2+BN2成立吗？答： （填“成立”或“不成立”）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】修建某一建筑时，若请甲、乙两个工程队同时施工，8天可以完成，需付两队费用共3520元；若先请甲队单独做6天，再请乙队单独做12天可以完成，需付两队费用共3480元，问：
（1）甲、乙两队每天费用各为多少？
（2）若单独请某队完成工程，则单独请哪队施工费用较少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果三角形的每条边都扩大为原来的5倍，那么三角形的每个角
A. 都扩大为原来的5倍 B. 都扩大为原来的10倍
C. 都扩大为原来的25倍 D. 都与原来相等
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，在矩形ABCD中，AB＝4 cm，BC＝8 cm，AC的垂直平分线EF分别交AD，BC于点E，F，垂足为O.
(1)如图①，连接AF，CE，试说明四边形AFCE为菱形，并求AF的长；
(2)如图②，动点P，Q分别从A，C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，已知点P的速度为5 cm/s，点Q的速度为4 cm/s，运动时间为t s，当以A，C，P，Q四点为顶点的四边形是平行四边形时，求t的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com