
【题目】如图,正方形![]() 中,点
中,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,连接
的中点,连接![]() ,若点
,若点![]() 为
为![]() 延长线上一动点,连接
延长线上一动点,连接![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心,逆时针旋转
为旋转中心,逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,则
,则![]() 、
、![]() 、
、![]() 三者之间的数量关系为________.
三者之间的数量关系为________.

【答案】![]() .
.
【解析】
取BC的中点G,连接FG,根据同角的余角相等求出∠1=∠3,然后利用“边角边”证明△FQE和△FPG全等,根据全等三角形对应边相等可得QE=FG,BF=BG,再根据BG+GP=BP等量代换即可得证.
如图,取BC的中点G,连接FG,
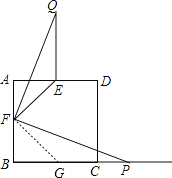
∵点E、F、G分别是正方形边AD、AB、BC的中点,
∴△AEF和△BGD是两个全等的等腰直角三角形.
∴EF=FG,∠AFE=∠BFG=45°.
∴∠EFG=90°,即EF⊥FG.
根据旋转的性质,FP=FQ,∠PFQ=90°.
∴∠GFP=∠GFE-∠EFP=90°-∠EFP,
∠EFQ=∠PFQ-∠EFP=90°-∠EFP.
∴∠GFP=∠EFQ.
在△FQE和△FPG中,
∵EF=GF,∠EFQ=∠GFP,FQ=FP,
∴△FQE≌△FPG(SAS).
∴EQ=GP.
∴EF=GF=![]() GB=
GB=![]() (BP-GP)=
(BP-GP)=![]() (BP-EQ),
(BP-EQ),
故答案为:EF=![]() (BP-EQ).
(BP-EQ).


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分9分)如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.

(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实党中央“长江大保护”新发展理念,我市持续推进长江岸线保护,还洞庭湖和长江水清岸绿的自然生态原貌.某工程队负责对一面积为33000平方米的非法砂石码头进行拆除,回填土方和复绿施工,为了缩短工期,该工程队增加了人力和设备,实际工作效率比原计划每天提高了20%,结果提前11天完成任务,求实际平均每天施工多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了发展乡村旅游,某村准备在河道上修一座与河道垂直的桥,如图(1)所示,直线l,m代表河流的两岸河道,且l∥m,点A是某村自助农场的所在地,点B是某村游乐场所在地.

问题1:造桥选址桥准备选在到A,B两地的距离之和刚好为最小的点C处,即在直线l上找一点C,使AC+BC的值为最小.请利用你所学的知识在图(1)中作出点C的位置,并简单说明你所设计方案的原理;
问题2:测量河宽:在测量河道的宽度时施工队在河道南侧的开阔地用以下方法(如图2所示):①作CD⊥l,与河对岸的直线m相交于D;②在直线m上取E,F两点,使得DE=EF=10米;③过点F作m的垂线FG,使得点G与C,E两点在同一直线上;④测量FG的长度为20米.请你确定河道的宽度,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,5),B(12,0),在y轴负半轴上取点E,使OA=EO,作∠CEF=∠AEB,直线CO交BA的延长线于点D.

(1)根据题意,可求得OE= ;
(2)求证:△ADO≌△ECO;
(3)动点P从E出发沿E﹣O﹣B路线运动速度为每秒1个单位,到B点处停止运动;动点Q从B出发沿B﹣O﹣E运动速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间△OPM与△OQN全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条船上午![]() 点在
点在![]() 处望见西南方向有一座灯塔
处望见西南方向有一座灯塔![]() (如图),此时测得船和灯塔相距
(如图),此时测得船和灯塔相距![]() 海里,船以每小时
海里,船以每小时![]() 海里的速度向南偏西
海里的速度向南偏西![]() 的方向航行到
的方向航行到![]() 处,这时望见灯塔在船的正北方向.(参考数据:
处,这时望见灯塔在船的正北方向.(参考数据:![]() ,
,![]() ).
).

![]() 求几点钟船到达
求几点钟船到达![]() 处;
处;
![]() 求船到达
求船到达![]() 处时与灯塔
处时与灯塔![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
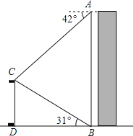
【题目】如图,某校数学兴趣小组在楼![]() 的顶部
的顶部![]() 处测得该楼正前方旗杆
处测得该楼正前方旗杆![]() 的顶端
的顶端![]() 的俯角为
的俯角为![]() ,在楼
,在楼![]() 的底部
的底部![]() 处测得旗杆
处测得旗杆![]() 的顶端
的顶端![]() 的仰角为
的仰角为![]() ,已知旗杆
,已知旗杆![]() 的高度为
的高度为![]() ,根据测得的数据,计算楼
,根据测得的数据,计算楼![]() 的高度(结果保留整数).
的高度(结果保留整数).
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (x>0,m≠0)的图象交于点C,与x轴、y轴分别交于点D、B,已知OB=3,点C的横坐标为4,cos∠0BD=
(x>0,m≠0)的图象交于点C,与x轴、y轴分别交于点D、B,已知OB=3,点C的横坐标为4,cos∠0BD=![]()
(1)求一次函数及反比例函数的表达式;
(2)将一次函数图象向下平移,使其经过原点O,与反比例函数图象在第四象限内的交点为A,连接AC,求四边形OACB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是( )

A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时,慢车距离乙地100千米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com