
【题目】如图,已知![]() 的半径为1,
的半径为1,![]() 是
是![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线
的切线![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 交
交![]() 于
于![]() 点,四边形
点,四边形![]() 是平行四边形.
是平行四边形.

(1)求![]() 的长:
的长:
(2)![]() 是
是![]() 的切线吗?若是,给出证明;若不是,说明理由.
的切线吗?若是,给出证明;若不是,说明理由.
【答案】(1)2;(2)是,理由见解析
【解析】
(1)连接BD,由DE是![]() 的直径,利用直径所对的圆周角为直角可知:∠DBE=90°,由平行四边形的性质可知:BC∥OE,BC=OE=1,在Rt△ABD中,利用直角三角形斜边中线定理可得AD的长;
的直径,利用直径所对的圆周角为直角可知:∠DBE=90°,由平行四边形的性质可知:BC∥OE,BC=OE=1,在Rt△ABD中,利用直角三角形斜边中线定理可得AD的长;
(2)连接OB,由BC∥OD,BC=OD,可得四边形BCDO是平行四边形,根据切线的性质可知:OD⊥AD,进而得到四边形BCDO是矩形,由矩形的性质可知OB⊥CB,继而求证BC为圆![]() 的切线.
的切线.
(1)如图,连接![]() ,
,
∵![]() 是直径,
是直径,
∴![]() ,
,
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
, ![]() ,
,
在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
(2)是,理由如下:
如图,连接![]() .
.
∵![]() ,
, ![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∵![]() 为圆
为圆![]() 的切线,
的切线,
∴![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴则![]() 为圆
为圆![]() 的切线.
的切线.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以![]() cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC![]() CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
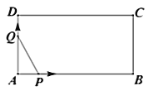
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发以
点出发以![]() /秒向终点
/秒向终点![]() 运动,动点
运动,动点![]() 同时从
同时从![]() 点出发以
点出发以![]() /秒按
/秒按![]()
![]() 的方向在边
的方向在边![]() ,
,![]() ,
,![]() 上运动,设运动时间为
上运动,设运动时间为![]() (秒),那么
(秒),那么![]() 的面积
的面积![]() 随着时间
随着时间![]() (秒)变化的函数图象大致为( )
(秒)变化的函数图象大致为( )
A.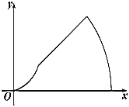 B.
B.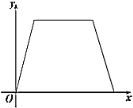 C.
C. D.
D.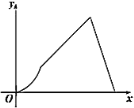
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
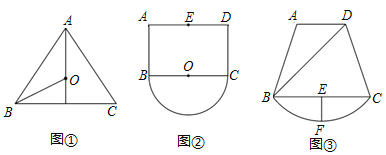
(1)如图①,在△ABC中,AB=AC=10,BC=12,点O是△ABC的外接圆的圆心,则OB的长为
问题探究
(2)如图②,已知矩形ABCD,AB=4,AD=6,点E为AD的中点,以BC为直径作半圆O,点P为半圆O上一动点,求E、P之间的最大距离;
问题解决
(3)某地有一块如图③所示的果园,果园是由四边形ABCD和弦CB与其所对的劣弧场地组成的,果园主人现要从入口D到![]() 上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120
上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120![]() 米,BC=160米,过弦BC的中点E作EF⊥BC交
米,BC=160米,过弦BC的中点E作EF⊥BC交![]() 于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图,把经过抛物线![]() (
(![]() ,
,![]() ,
, ![]() ,
,![]() 为常数)与
为常数)与![]() 轴的交点
轴的交点![]() 和顶点
和顶点![]() 的直线称为抛物线的“伴线”,若抛物线与
的直线称为抛物线的“伴线”,若抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的右侧),经过点
的右侧),经过点![]() 和点
和点![]() 的直线称为抛物线的“标线”.
的直线称为抛物线的“标线”.
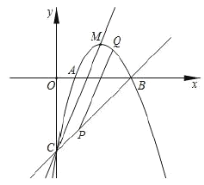
(1)已知抛物线![]() ,求伴线的解析式.
,求伴线的解析式.
(2)若伴线为![]() ,标线为
,标线为![]() ,
,
①求抛物线的解析式;
②设![]() 为“标线”上一动点,过
为“标线”上一动点,过![]() 作
作![]() 平行于“伴线”,交“标线”上方的抛物线于
平行于“伴线”,交“标线”上方的抛物线于![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A.平均数是6
B.中位数是6.5
C.众数是7
D.平均每周锻炼超过6小时的人数占该班人数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前夕,某批发部从厂家购进A、B两种礼盒,已知购进2个A礼盒和3个B礼盒共花520元;购进3个A礼盒和2个B礼盒共花费480元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该批发部经理购进这两种礼盒恰好用去4800元购进A种礼盒最多18个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)已知销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使A、B两种礼盒全部售出后所有方案获利均相同,m的值应是多少?此时这个批发部获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )

A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com