练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．下列运算中，结果正确的是（　　）
    A．（a3）2=a6B．（ab）3=a3bC．a•a3=a3D．a8÷a4=a2

    分析 根据整式的运算法则即可求出答案．

    解答 解：（B）原式=a3b3，故B错误；
    （C）原式=a4，故C错误；
    （D）原式=a4，故D错误

    点评 本题考查整式的运算法则，解题的关键是熟练运用整式的运算法则，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．小王同学准备筹集资金为贫困山区儿童捐款，打算从淘宝网上购进一批闪光发箍和荧光棒在某演唱会现场出售，其中闪光发箍的购买价格为6元/个，荧光棒的购买价格为8元/个．
    （1）小王计划购进闪光发箍和荧光棒共120个，且将闪光发箍加价40%、荧光棒加价20%后出售．当所有物品售完后，若利润不低于256元，则小王至少应购买闪光发箍多少个？
    （2）小王调整了方案，决定将闪光发箍的售价在进价的基础上上涨（a+10）%、荧光棒的售价在进价基础上上涨a%，在（1）中闪光发箍购买量取得最小值的情况下，将闪光发箍的购买量提高$\frac{5}{3}$a%，而荧光棒的购买量保持不变，则全部售出后，最终可获利384元，请求出a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列计算正确的是（　　）
    A．a3+a2=2a5B．a3•a2=a6C．a3÷a2=aD．（a3）2=a9

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

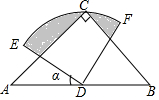    12．如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠ADE=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（　　）
    A．由小变大B．由大变小
    C．不变D．先由小变大，后由大变小

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，正比例函数y1=k1x和一次函数y2=k2x+b的图象相交于点A（2，1），当x＜2时，y1＜y2．（填“＞”或“＜”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知AB∥CD，AD与BC相交于点O．若$\frac{BO}{OC}$=$\frac{2}{3}$，AD=10，则AO=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列关于函数y=x2-6x+10的四个命题：
    ①当x=0时，y有最小值10；
    ②n为任意实数，x=3+n时的函数值大于x=3-n时的函数值；
    ③若n＞3，且n是整数，当n≤x≤n+1时，y的整数值有（2n-4）个；
    ④若函数图象过点（a，y0）和（b，y0+1），其中a＞0，b＞0，则a＜b．
    其中真命题的序号是（　　）
    A．①B．②C．③D．④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．问题呈现：
    如图1，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上，AE=DG，求证：2S四边形EFGH=S矩形ABCD．（S表示面积）
    实验探究：
    某数学实验小组发现：若图1中AH≠BF，点G在CD上移动时，上述结论会发生变化，分别过点E、G作BC边的平行线，再分别过点F、H作AB边的平行线，四条平行线分别相交于点A1、B1、C1、D1，得到矩形A1B1C1D1．
    如图2，当AH＞BF时，若将点G向点C靠近（DG＞AE），经过探索，发现：2S四边形EFGH=S矩形ABCD+S${\;}_{矩形{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$．
    如图3，当AH＞BF时，若将点G向点D靠近（DG＜AE），请探索S四边形EFGH、S矩形ABCD与S${\;}_{矩形{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$之间的数量关系，并说明理由．
    迁移应用：
    请直接应用“实验探究”中发现的结论解答下列问题：
    （1）如图4，点E、F、G、H分别是面积为25的正方形ABCD各边上的点，已知AH＞BF，AE＞DG，S四边形EFGH=11，HF=$\sqrt{29}$，求EG的长．
    （2）如图5，在矩形ABCD中，AB=3，AD=5，点E、H分别在边AB、AD上，BE=1，DH=2，点F、G分别是边BC、CD上的动点，且FG=$\sqrt{10}$，连接EF、HG，请直接写出四边形EFGH面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．设直线x=1是函数y=ax2+bx+c（a，b，c是实数，且a＜0）的图象的对称轴，（　　）
    A．若m＞1，则（m-1）a+b＞0B．若m＞1，则（m-1）a+b＜0
    C．若m＜1，则（m+1）a+b＞0D．若m＜1，则（m+1）a+b＜0

    查看答案和解析>>

    同步练习册答案