
【题目】如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2 ![]() ;③当AD=2时,EF与半圆相切;④若点F恰好落在
;③当AD=2时,EF与半圆相切;④若点F恰好落在 ![]() 上,则AD=2
上,则AD=2 ![]() ;⑤当点D从点A运动到点B时,线段EF扫过的面积是16
;⑤当点D从点A运动到点B时,线段EF扫过的面积是16 ![]() .其中正确结论的序号是 .
.其中正确结论的序号是 . 
【答案】①、③、⑤
【解析】解:①连接CD,如图1所示. 
∵点E与点D关于AC对称,
∴CE=CD.
∴∠E=∠CDE.
∵DF⊥DE,
∴∠EDF=90°.
∴∠E+∠F=90°,∠CDE+∠CDF=90°.
∴∠F=∠CDF.
∴CD=CF.
∴CE=CD=CF.
∴结论“CE=CF”正确.
②当CD⊥AB时,如图2所示.
∵AB是半圆的直径,
∴∠ACB=90°.
∵AB=8,∠CBA=30°,
∴∠CAB=60°,AC=4,BC=4 ![]() .
.
∵CD⊥AB,∠CBA=30°,
∴CD= ![]() BC=2
BC=2 ![]() .
.
根据“点到直线之间,垂线段最短”可得:
点D在线段AB上运动时,CD的最小值为2 ![]() .
.
∵CE=CD=CF,
∴EF=2CD.
∴线段EF的最小值为4 ![]() .
.
∴结论“线段EF的最小值为2 ![]() ”错误.
”错误.
③当AD=2时,连接OC,如图3所示.
∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形.
∴CA=CO,∠ACO=60°.
∵AO=4,AD=2,
∴DO=2.
∴AD=DO.
∴∠ACD=∠OCD=30°.
∵点E与点D关于AC对称,
∴∠ECA=∠DCA.
∴∠ECA=30°.
∴∠ECO=90°.
∴OC⊥EF.
∵EF经过半径OC的外端,且OC⊥EF,
∴EF与半圆相切.
∴结论“EF与半圆相切”正确.
④当点F恰好落在 ![]() 上时,连接FB、AF,如图4所示.
上时,连接FB、AF,如图4所示.
∵点E与点D关于AC对称,
∴ED⊥AC.
∴∠AGD=90°.
∴∠AGD=∠ACB.
∴ED∥BC.
∴△FHC∽△FDE.
∴ ![]() .
.
∵FC= ![]() EF,
EF,
∴FH= ![]() FD.
FD.
∴FH=DH.
∵DE∥BC,
∴∠FHC=∠FDE=90°.
∴BF=BD.
∴∠FBH=∠DBH=30°.
∴∠FBD=60°.
∵AB是半圆的直径,
∴∠AFB=90°.
∴∠FAB=30°.
∴FB= ![]() AB=4.
AB=4.
∴DB=4.
∴AD=AB﹣DB=4.
∴结论“AD=2 ![]() ”错误.
”错误.
⑤∵点D与点E关于AC对称,
点D与点F关于BC对称,
∴当点D从点A运动到点B时,
点E的运动路径AM与AB关于AC对称,
点F的运动路径NB与AB关于BC对称.
∴EF扫过的图形就是图5中阴影部分.
∴S阴影=2S△ABC
=2× ![]() ACBC
ACBC
=ACBC
=4×4 ![]()
=16 ![]() .
.
∴EF扫过的面积为16 ![]() .
.
∴结论“EF扫过的面积为16 ![]() ”正确.
”正确.
所以答案是:①、③、⑤.
【考点精析】本题主要考查了垂线段最短和平行线的判定与性质的相关知识点,需要掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1). 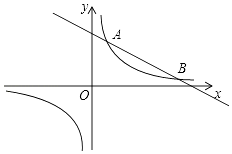
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点![]() 按如图方式叠放在一起,当
按如图方式叠放在一起,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示:![]() ,
,![]() ,
,![]() .
.

(1)①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出![]() 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且![]() =
=![]() ,连接AC,AD,延长AD交BM于点E.
,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形.
(2)连接OE,若DE=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( ) 
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=﹣ ![]() (x<0)与y=
(x<0)与y= ![]() (x>0)的图象上,则ABCD的面积为 .
(x>0)的图象上,则ABCD的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3 , 则下列结论不一定成立的是( ) 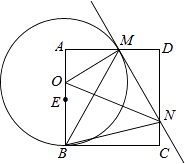
A.S1>S2+S3
B.△AOM∽△DMN
C.∠MBN=45°
D.MN=AM+CN
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com