
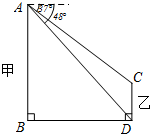
 如图,线段AB,CD表示甲、乙两幢居民楼的高,两楼间的距离BD是60米.某人站在A处测得C点的俯角为37°,D点的俯角为48°(人的身高忽略不计),求乙楼的高度CD.(参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin48°≈$\frac{7}{10}$,tan48°≈$\frac{11}{10}$)
如图,线段AB,CD表示甲、乙两幢居民楼的高,两楼间的距离BD是60米.某人站在A处测得C点的俯角为37°,D点的俯角为48°(人的身高忽略不计),求乙楼的高度CD.(参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin48°≈$\frac{7}{10}$,tan48°≈$\frac{11}{10}$) 分析 过点C作CE⊥AB交AB于点E,在直角△ADB中利用三角函数求得AB的长,然后在直角△AEC中求得AE的长,即可求解.
解答  解:过点C作CE⊥AB交AB于点E,
解:过点C作CE⊥AB交AB于点E,
则四边形EBDC为矩形,
∴BE=CD CE=BD=60,
如图,根据题意可得,
∠ADB=48°,∠ACE=37°,
∵$tan48°=\frac{AB}{BD}$,
在Rt△ADB中,
则AB=tan48°•BD≈$\frac{11}{10}×60=66$(米),
∵$tan37°=\frac{AE}{CE}$,
在Rt△ACE中,
则AE=tan37°•CE≈$\frac{3}{4}×60=45$(米),
∴CD=BE=AB-AE=66-45=21(米),
∴乙楼的高度CD为21米.
点评 本题考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )| A. | 15° | B. | 17.5° | C. | 20° | D. | 22.5° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
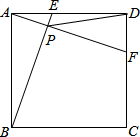 如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,则线段DP的最小值为$\sqrt{5}$-1.
如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,则线段DP的最小值为$\sqrt{5}$-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com