

 .
.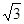 ,根据三角形的面积公式求△DFH的面积,即可求出答案.
,根据三角形的面积公式求△DFH的面积,即可求出答案.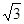 ,
,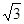 ,CH=BF=1,
,CH=BF=1,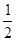 DH?FH=4
DH?FH=4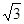 ,
,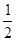 S△DHF=2
S△DHF=2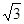 .
.

科目:初中数学 来源:不详 题型:解答题
 面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.
面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化. (不要求写出自变量x的取值范围);
(不要求写出自变量x的取值范围);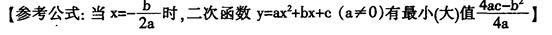
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 果DE2=BE·CE,求证四边形ABFC是矩形.
果DE2=BE·CE,求证四边形ABFC是矩形.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com